Data Management
We learn three main things during this week’s lab session:
- Loading packages
- Importing data sets from a file
- Summarizing categorical and numerical data
0. Preparation (Creating an R project)
Before we begin, do the following:
-
If you haven’t done so already, create a folder named “POLI502” somewhere on your computer (could be on your desktop, documents folder, etc.)
-
Download all the files for today from Blackboard, including POLI502-week5-JointExercise.R, POLI502-week5-IndividualExercise.R, world.csv, world codebook.pdf
-
Move all the four files you downloaded to your own POLI502 folder.
-
Create a R project in the POLI502 folder if you haven’t done so already
1. Loading R packages
We have been using some R functions such as summary(), data.frame(), sqrt(), etc. These simple functions come with the base R installation and so we can use them without doing any additional installation.
One of the great advantages of R is the availability of “packages” – a collection of additional functions. To use a package, we need to do two things:
- Install it
- Load it
Installation must be done just once per computer. For example, once you install a package called ggplot2 to your computer, you won’t need to install it ever again. However, you still need to load the package each time you start a new R session.
(1) Installing a package
To install an R package, we use the install.packages function.
# install.packages("ggplot2", dependencies = TRUE)
ggplot2 is the name of the package we install. We put the dependencies = TRUE option here because we want to install all the additional packages that ggplot2 depends on.
Some packages depend on other packages. For example, the ggplot2 package depends on eight other packages (plyr, digest, grid, gtable, reshape2, scales, proto, and MASS), each of which might also depend on yet other packages. Loading the ggplot2 package requires that we also load all the packages that it depends on, which means that we need to install all these packages. The dependencies = TRUE option does exactly that.
Installation might take a while, but the good news is that you don’t need to do this again for ggplot2 (Of course, you may have to install some other packages in the future).
Once the installation is done, you can now load the ggplot2 package.
library(ggplot2)
If you don’t get any error message, it means you have successfully loaded this package.
Remember that loading must be done every time we start R (R studio).
(2) Loading a package
To load a package, we use the library function. Let’s load a package called ggplot2, which contains a lot of graphic functions.
library(ggplot2)
What happened on your computer?
If you are using your own computer, you probably got an error message saying Error in library(ggplot2) : there is no package called ‘ggplot2’.
This happened because we haven’t done (1).
If, on the other hand, you are using a lab computer, you probably didn’t get any error message. This is because someone has already installed this package to the computer you are using. Remember we need to install a package once per computer.
2. Importing data sets from a file
We have learned how to work with data.frame objects last week. We even created a mini data set using the data.frame function. In practice, we work with data sets that are much larger than the mini data set we created. Moreover, we usually import such data sets from a file, not by typing in information on our own. To read in (=import) a data set from a file, we use read.XXX functions, such as
read.csv: Comma-separated text fileread.table: Tab-separated text fileread.dta: Stata fileread.spss: SPSS fileread.xlsx: Excel file
We will use the read.csv function today. We will learn others in the future.
Let’s use the read.csv function and import the “World” data set we discussed in the lecture.
# path = "/Users/howardliu/Library/CloudStorage/Dropbox/myjobs/UofSC_South-carolina/SC_teaching/POLI502/502_week5_measurement/lab-week5-describe-data/"
# world.data <- read.csv(paste0(path, "world.csv"))
world.data <- read.csv("world.csv")
What happened on your computer?
If you don’t get any error message, that’s perfect. You have successfully imported a data set from the world.csv file.
If, on other other hand, you get an error message that starts with Error in file(file, "rt") : cannot open the connection, that could be because of one or more of the following reasons:
- You haven’t downloaded the world.csv file from Blackboard or from the course website;
- You haven’t moved the world.csv file to the POLI502 folder;
- You have done both (1) and (2), but R doesn’t know where POLI502 is.
Let’s first do (1) and (2) if you haven’t done so. Now we will see how to resolve (3).
Setting the path
When you do some file operations in R (such as loading a data set from a file, or saving data, graphs, or outputs into a file), we need to tell R the exact location (address) of the file.
Locations on a computer are called “path”. A path is like an address. It identifies the location of files and folders on a computer.
When using functions such as read.csv, R looks for files contained in one folder and one folder only. The folder that R thinks R is located currently is called “current directory” or “working directory”.
“Directory” is just another name for “folder”. So, the working directory refers to the folder that R searches when trying to open a file.
When you open R Studio by double-clicking on a script file (such as the present file POLI502-week5-JointExercise.R), the working directory is automatically set to the folder that contains the script file.
Therefore, if you have opened this 502-week5-JointExercise.R file saved today, then the working directory has been correctly set to POLI502.
If not, we need to change it.
To find out what folder R is currently residing, we use the getwd function, short for “get W(orking) D(irectory)”
getwd() this is the magic working in a R project; you don’t need to setwd each time and it saves time for your collaborator
If you are on a lab computer, R will tell you something like: m:/pc/desktop/POLI502
If you are on a Mac computer, R will tell you something like: Users/howardliu/Desktop/POLI502 or Users/howardliu/Documents/POLI502
To change the working directory, we use the setwd function, short for “set W(orking) D(irectory)”
If you are on a lab computer, execute the following. Do not execute it if you are on your own computer.
# setwd("m:/pc/desktop/POLI502")
If you are using your own Mac computer, execute the following: You need to replace “daina” with your own username.You may also need to replace “Desktop” with “Documents” or something, depending on where you created the POLI502 folder.
# setwd("/Users/howardliu/Dropbox/POLI502")
If you are using your own Windows computer, the exact path would depend on how your computer is configured, so you probably want to ask for your TA’s help.
One option is to close R Studio once, and re-open it by double-clicking on the POLI502-week5-JointExercise.R file.
Now, let’s see if the path is set correctly.
getwd()
## [1] "/Users/howardliu/methodsPol/content/class"
If it shows the location of the POLI502 folder that contains the world.csv file, we should be able to execute the following again.
# View(world.data)
Look what we are doing above. We are creating a new object named world.data and its contents is the result of applying the read.csv function.
Note: If you load data in a quarto doc (.qmd), quarto uses a relative directory, meaning it doesn’t allow you to set a different working dir for your data file. Currently, you would need to save the data file in the same folder as your quarto file so the data can be loaded.
Understanding pipe operator %>% in R
Nice reference on pipes here
The pipe operator makes it possible to easily chain a sequence of calculations.
first, install it from this package
library(magrittr)
x <- -300
round((sqrt(abs(x))))
## [1] 17
x <- c(0.109, 0.359, 0.63, 0.996, 0.515, 0.142, 0.017, 0.829, 0.907)
Compute the logarithm of x, return suitably lagged and iterated differences, compute the exponential function and round the result
round(exp(diff(log(x))), 1)
## [1] 3.3 1.8 1.6 0.5 0.3 0.1 48.8 1.1
round(exp(diff(log(x))), 1)
## [1] 3.3 1.8 1.6 0.5 0.3 0.1 48.8 1.1
x %>% log %>% diff %>% exp %>% round(., 1)
## [1] 3.3 1.8 1.6 0.5 0.3 0.1 48.8 1.1
The hotkey for %>% is Command + shift + m
In the following, I’ll show you situations where using pipes makes your life easier
Difference between base R |> (native pipes) and magrittr %>% (pipes)
While |> and %>% behave identically for simple cases, there are a few crucial differences. These are most likely to affect you if you’re a long-term user of %>% who has taken advantage of some of the more advanced features. But they’re still good to know about even if you’ve never used %>% because you’re likely to encounter some of them when reading wild-caught code
%>%allows you to drop the parentheses when calling a function with no other arguments;|>always requires the parentheses.
# library(magrittr)
library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ lubridate 1.9.3 ✔ tibble 3.2.1
## ✔ purrr 1.0.2 ✔ tidyr 1.3.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ tidyr::extract() masks magrittr::extract()
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ✖ purrr::set_names() masks magrittr::set_names()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
world.data %>%
filter(!is.na(democ_regime)) %>%
.$country %>%
head()
## [1] "Afghanistan" "Albania" "Algeria"
## [4] "Andorra" "Angola" "Antigua & Barbuda"
world.data |>
filter(!is.na(democ_regime)) |>
head()
## country colony confidence decentralization dem_other
## 1 Afghanistan UK NA NA 10.5
## 2 Albania Soviet Union 49.33593 0.74 63.0
## 3 Algeria France 52.05573 NA 40.8
## 4 Andorra Spain NA NA 100.0
## 5 Angola Portugal NA NA 40.8
## 6 Antigua & Barbuda UK NA NA 87.5
## dem_other5 democ_regime district_size3 durable effectiveness enpp_3
## 1 10% No single member 4 13.71158
## 2 Approx 60% Yes 3 35.46099 1-3 parties
## 3 Approx 40% No 6 or more members 5 32.62411
## 4 100% Yes NA 78.72340
## 5 Approx 40% No 3 19.14894
## 6 Approx 90% Yes single member NA 59.81088 1-3 parties
## eu fhrate04_rev fhrate08_rev frac_eth frac_eth3 free_business
## 1 Not member 2.5 3 0.7693 High NA
## 2 Not member 5 8 0.2204 Low 68.0
## 3 Not member 2.5 3 0.3394 Medium 71.2
## 4 Not member Most free 12 0.7139 High NA
## 5 Not member 2.5 3 0.7867 High 43.4
## 6 Not member 6 10 0.1643 Low NA
## free_corrupt free_finance free_fiscal free_govspend free_invest free_labor
## 1 NA NA NA NA NA NA
## 2 34 70 92.6 74.2 70 52.1
## 3 32 30 83.5 73.4 45 56.4
## 4 NA NA NA NA NA NA
## 5 19 40 85.1 62.8 35 45.2
## 6 NA NA NA NA NA NA
## free_monetary free_overall free_property free_trade gdp08 gdp_10_thou
## 1 NA NA NA NA 30.6 NA
## 2 78.7 66.0 35 85.8 24.3 0.1535
## 3 77.2 56.9 30 70.7 276.0 0.1785
## 4 NA NA NA NA NA NA
## 5 62.6 48.4 20 70.4 106.3 0.0857
## 6 NA NA NA NA NA 1.0449
## gdp_cap2 gdp_cap3 gdppcap08 gender_equal3 gini04 gini08 hi_gdp indy
## 1 NA NA NA 1919
## 2 Low Middle 7715 28.2 31.1 Low GDP 1991
## 3 Low Middle 8033 35.3 35.3 Low GDP 1962
## 4 NA NA NA 1278
## 5 Low Middle 5899 NA NA Low GDP 1975
## 6 High High NA NA NA High GDP 1981
## oecd old2006 old2003 pmat12_3 pop03 pop08 pop08_3
## 1 Not member NA NA NA 27.4 >=16.8 mil
## 2 Not member 8.479821 7.278363 Low post-mat 3169064 3.1 <=4.3 mil
## 3 Not member 4.578136 4.045199 31832610 34.4 >=16.8 mil
## 4 Not member NA NA 66000 NA
## 5 Not member 2.450295 2.930542 13522110 18.0 >=16.8 mil
## 6 Not member NA 8.186610 78580 NA
## popcat3 pr_sys protact3 regime_type3 region sources
## 1 Moderate (1-29m) No Dictatorship Middle East NA
## 2 Moderate (1-29m) No Moderate Parliamentary democ C&E Europe NA
## 3 Moderate (1-29m) Yes Dictatorship Africa NA
## 4 Small (under 1m) No Parliamentary democ W. Europe NA
## 5 Moderate (1-29m) Yes Dictatorship Africa NA
## 6 Small (under 1m) No Parliamentary democ S. America NA
## typerel unions urban03 urban06 vi_rel3 votevap00s women05 women09
## 1 Muslim NA NA 23.28 NA NA 27.7
## 2 Muslim NA 44.2390 46.14 20-50% 59.56 6.4 16.4
## 3 Muslim NA 58.8302 63.94 >50% NA NA 7.7
## 4 Roman Catholic NA 91.7404 90.28 20.95 14.3 35.7
## 5 Roman Catholic NA 36.1806 53.96 NA NA 37.3
## 6 Protestant NA 37.7566 39.60 76.34 10.5 10.5
## womyear womyear2 yng2003 young06
## 1 NA NA NA
## 2 1920 1944 or before 27.34834 26.35428
## 3 1962 After 1944 33.91887 28.94154
## 4 1973 After 1944 NA NA
## 5 1975 After 1944 47.62524 46.32196
## 6 1951 After 1944 20.66509 NA
# .$country
%>%allows you to start a pipe with.to create a function rather than immediately executing the pipe; this is not supported by the base pipe.
Exploring a data set
Whenever you read in a data set from a file, it’s always a good idea to take a look at it first to have an idea about what it looks like. There are a few functions that will let us take a look at the data set. The dim function tells us the dimension (the number of rows and the number of columns)
dim(world.data)
## [1] 191 62
So this contains 191 rows (observations) and 62 columns (variables)
The head and tail functions let us see the first or last 5 rows of the data set.
# world.data
# head(world.data,10)
# tail(world.data,8)
Or we can do this using the square brackets
world.data[1:10, 1:5]
## country colony confidence decentralization dem_other
## 1 Afghanistan UK NA NA 10.5
## 2 Albania Soviet Union 49.335926 0.74 63.0
## 3 Algeria France 52.055735 NA 40.8
## 4 Andorra Spain NA NA 100.0
## 5 Angola Portugal NA NA 40.8
## 6 Antigua & Barbuda UK NA NA 87.5
## 7 Argentina Spain 7.299325 2.40 87.5
## 8 Armenia Soviet Union 27.132735 NA 63.0
## 9 Australia UK 46.838886 1.74 58.3
## 10 Austria Other 49.680190 1.81 100.0
This tells R to show the first 10 rows and first 5 columns. We can easily see that country is the unit of observation. We can also see that there are variables such as colony, confidence, decentralization, and dem_other.
When working with a large data set like this one, you may want to use the spreadsheet view (just like Excel). To do so, we use the View function, which opens a spreadsheet tab in the script pane.
# View(world.data)
3. Summarizing data
Now we will use numerical and graphical methods to summarize data. As we learned in the lecture, we will need different methods for different types of data (categorical or numerical).
Categorical variables
As we saw in the lecture, there is a variable called “colony” in the data set that records the former colonial master country for each observation. Let’s see how to summarize the information contained in this variable.
To access a variable included in a data frame object, we use the $ symbol.
# world.data $ colony
Now R shows the values of this variable for all the 191 observations. We can see that this variable takes values such as UK, Soviet Union, France, etc. To see what value each country (each row) takes, we may want to see the “country” variable and the “colony” variables at the same time. Since the “country” variable is stored in the first column and the “colony” variable in the second column, we can do the following:
# world.data[, 1:2]
This shows the first and second columns for all rows. Alternatively, we can do the following to get the same output.
world.data[ c("country", "colony") ]
## country colony
## 1 Afghanistan UK
## 2 Albania Soviet Union
## 3 Algeria France
## 4 Andorra Spain
## 5 Angola Portugal
## 6 Antigua & Barbuda UK
## 7 Argentina Spain
## 8 Armenia Soviet Union
## 9 Australia UK
## 10 Austria Other
## 11 Azerbaijan Soviet Union
## 12 Bahamas UK
## 13 Bahrain UK
## 14 Bangladesh Other
## 15 Barbados UK
## 16 Belarus Soviet Union
## 17 Belgium Netherlands
## 18 Belize UK
## 19 Benin France
## 20 Bhutan Other
## 21 Bolivia Spain
## 22 Bosnia Soviet Union
## 23 Botswana UK
## 24 Brazil Portugal
## 25 Brunei Darussalam UK
## 26 Bulgaria Soviet Union
## 27 Burkina Faso France
## 28 Burundi Belgium
## 29 Cambodia France
## 30 Cameroon France
## 31 Canada UK
## 32 Cape Verde Portugal
## 33 Central African Republic France
## 34 Chad France
## 35 Chile Spain
## 36 China none
## 37 Colombia France
## 38 Comoros France
## 39 Congo Brazzaville France
## 40 Congo Kinshasa Belgium
## 41 Costa Rica Spain
## 42 Cote d'Ivoire France
## 43 Croatia Soviet Union
## 44 Cuba Spain
## 45 Cyprus UK
## 46 Czech Republic Soviet Union
## 47 Denmark none
## 48 Djibouti France
## 49 Dominica UK
## 50 Dominican Rep Other
## 51 Ecuador Spain
## 52 Egypt UK
## 53 El Salvador Spain
## 54 Equatorial Guinea Spain
## 55 Eritrea Other
## 56 Estonia Soviet Union
## 57 Ethiopia none
## 58 Fiji UK
## 59 Finland none
## 60 France France
## 61 Gabon France
## 62 Gambia UK
## 63 Georgia Soviet Union
## 64 Germany none
## 65 Ghana UK
## 66 Greece Ottoman
## 67 Grenada UK
## 68 Guatemala Spain
## 69 Guinea-Bissau Spain
## 70 Guinea Portugal
## 71 Guyana UK
## 72 Haiti France
## 73 Honduras Spain
## 74 Hungary Soviet Union
## 75 Iceland none
## 76 India UK
## 77 Indonesia Netherlands
## 78 Iran none
## 79 Iraq UK
## 80 Ireland UK
## 81 Israel UK
## 82 Italy none
## 83 Jamaica UK
## 84 Japan none
## 85 Jordan UK
## 86 Kazakhstan Soviet Union
## 87 Kenya UK
## 88 Kiribati UK
## 89 Korea North Other
## 90 Korea South Other
## 91 Kuwait UK
## 92 Kyrgyzstan Soviet Union
## 93 Laos France
## 94 Latvia Soviet Union
## 95 Lebanon France
## 96 Lesotho UK
## 97 Liberia UK
## 98 Libya Other
## 99 Liechtenstein none
## 100 Lithuania Soviet Union
## 101 Luxembourg Netherlands
## 102 Macedonia Soviet Union
## 103 Madagascar France
## 104 Malawi UK
## 105 Malaysia UK
## 106 Maldives UK
## 107 Mali France
## 108 Malta UK
## 109 Marshall Islands none
## 110 Mauritania France
## 111 Mauritius UK
## 112 Mexico Spain
## 113 Micronesia, Fed Stat none
## 114 Moldova Soviet Union
## 115 Monaco none
## 116 Mongolia Other
## 117 Morocco France
## 118 Mozambique Portugal
## 119 Myanmar (Burma) UK
## 120 Namibia Other
## 121 Nauru UK
## 122 Nepal none
## 123 Netherlands Spain
## 124 New Zealand UK
## 125 Nicaragua Spain
## 126 Niger France
## 127 Nigeria UK
## 128 Norway none
## 129 Oman Portugal
## 130 Pakistan UK
## 131 Palau none
## 132 Panama Spain
## 133 Papua New Guinea Other
## 134 Paraguay Spain
## 135 Peru Spain
## 136 Philippines Spain
## 137 Poland Soviet Union
## 138 Portugal Portugal
## 139 Qatar UK
## 140 Romania Soviet Union
## 141 Russia Soviet Union
## 142 Rwanda Belgium
## 143 San Marino none
## 144 Sao Tome Portugal
## 145 Saudi Arabia UK
## 146 Senegal France
## 147 Seychelles UK
## 148 Sierra Leone UK
## 149 Singapore Other
## 150 Slovakia Soviet Union
## 151 Slovenia Soviet Union
## 152 Solomon Islands UK
## 153 Somalia UK
## 154 South Africa UK
## 155 Spain Spain
## 156 Sri Lanka UK
## 157 St. Kitts & Nevis UK
## 158 St. Lucia UK
## 159 St. Vincent & Grenadine UK
## 160 Sudan UK
## 161 Suriname Netherlands
## 162 Swaziland UK
## 163 Sweden none
## 164 Switzerland none
## 165 Syria France
## 166 Taiwan Other
## 167 Tajikistan Soviet Union
## 168 Tanzania UK
## 169 Thailand none
## 170 Togo France
## 171 Tonga UK
## 172 Trinidad UK
## 173 Tunisia France
## 174 Turkey Ottoman
## 175 Turkmenistan Soviet Union
## 176 Tuvalu UK
## 177 UAE UK
## 178 Uganda UK
## 179 Ukraine Soviet Union
## 180 United Kingdom UK
## 181 United States UK
## 182 Uruguay Other
## 183 Uzbekistan Soviet Union
## 184 Vanuatu France
## 185 Venezuela Spain
## 186 Vietnam France
## 187 Western Samoa Other
## 188 Yemen UK
## 189 Serbia & Montenegro Soviet Union
## 190 Zambia UK
## 191 Zimbabwe UK
You can see which country was formerly colonized by which country.
Now, going back to summarizing the colony variable, we will create what’s called a frequency table to summarize a nominal-level variable like this.
This will summarize this variable in a more concise way so we can easily see things like what are the “typical” values, how frequent these typical values appear, etc.
One way to create a frequency table is to use the table function, as follows
table(world.data $ colony)
##
## Belgium France Netherlands none Other Ottoman
## 3 28 4 20 15 2
## Portugal Soviet Union Spain UK
## 8 27 21 63
Alternatively, we can also use the summary function as well:
summary(world.data $ colony)
## Length Class Mode
## 191 character character
The output above nicely summarizes the information contained in the colony variable. We can see the (raw) frequencies with which each value is observed in the data set. For example, there are 3 observations (countries) that are former colonies of Belgium, 28 former colonies of France, 4 former colonies of the Netherlands, etc.
To make it more like the frequency table you saw in the lecture slide, we can make it vertical using the data.frame function
data.frame( table(world.data $ colony) )
## Var1 Freq
## 1 Belgium 3
## 2 France 28
## 3 Netherlands 4
## 4 none 20
## 5 Other 15
## 6 Ottoman 2
## 7 Portugal 8
## 8 Soviet Union 27
## 9 Spain 21
## 10 UK 63
tb <- world.data $ colony %>% table %>% data.frame()
Another way to summarize the information contained in a nominal-level variable is to create a bar chart, which is a graphical representation of a frequency table.
ggplot(world.data, aes(x = colony)) + geom_bar()
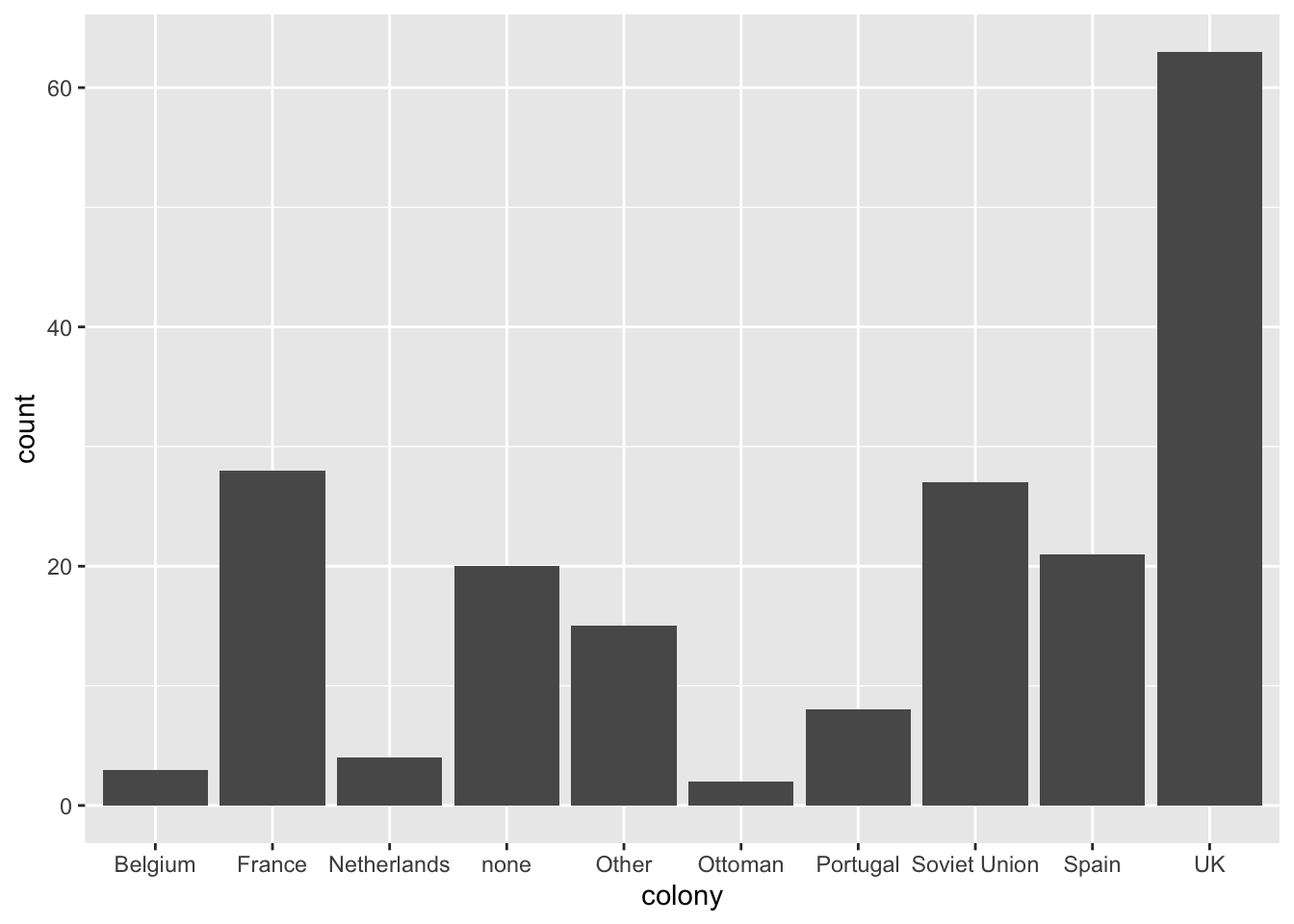
The first part tells R that world.data is the name of the data frame object that contains a variable(s) we want to plot.
The second part, the aes option (short for aesthetic) tells R which variable(s) we want to plot. We don’t need to enclose variable names with ““.
Finally, the last part, + geom_bar(), tells R that we want a bar chart. We will use geom_histogram() to create a histogram, geom_boxplot to create a box plot, geom_points() to create a scatterplot, etc. (More on this next week).
Numerical variables
This data set also contains a number of numerical variables. One of them is called “women09”, which we saw in the lecture.
world.data $ women09 %>% class
## [1] "numeric"
This variable records the percentage of women in the lower house of parliament for each country, measured in the year 2009.
To see what value each country has, we can do
# world.data[ c("country", "women09") ]
Let’s now summarize this variable. To summarize the information contained in a numeric (interval-level) variable like this one, we identify the central tendency (mean & median) and dispersion (range, inter-quartile range, standard deviation, variance), as we learned in the lecture.
The summary function gives us summary values including the five number summary mean, and the number of observations with missing values.
summary(world.data $ women09)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.00 9.70 15.55 17.18 22.95 56.30 11
# Min. = Q0 = minimum = 0th percentile
# 1st Qu. = Q1 = 1st quartile = 25th percentile = median of the lower half of the data
# Median = Q2 = median = 50th percentile
# Mean = mean (average)
# 3rd Qu. = Q3 = 3rd quartile = 75th percentile = median of the upper half of the data
# Max. = Q4 = 4th quartile = 100th percentile = maximum value
If we just want mean or median, we can use the mean and median functions. However, it won’t work if the variable contains some missing values
mean(world.data $ women09)
## [1] NA
median(world.data $ women09)
## [1] NA
What is a missing value? Look at the data on women09 again.
world.data[ c("country", "women09") ]
## country women09
## 1 Afghanistan 27.7
## 2 Albania 16.4
## 3 Algeria 7.7
## 4 Andorra 35.7
## 5 Angola 37.3
## 6 Antigua & Barbuda 10.5
## 7 Argentina 41.6
## 8 Armenia 8.4
## 9 Australia 26.7
## 10 Austria 27.9
## 11 Azerbaijan 11.4
## 12 Bahamas 12.2
## 13 Bahrain 2.5
## 14 Bangladesh 18.6
## 15 Barbados 10.0
## 16 Belarus 31.8
## 17 Belgium 35.3
## 18 Belize 0.0
## 19 Benin 10.8
## 20 Bhutan 8.5
## 21 Bolivia 16.9
## 22 Bosnia 11.9
## 23 Botswana 11.1
## 24 Brazil 9.0
## 25 Brunei Darussalam NA
## 26 Bulgaria 20.8
## 27 Burkina Faso 15.3
## 28 Burundi 30.5
## 29 Cambodia 16.3
## 30 Cameroon 13.9
## 31 Canada 22.1
## 32 Cape Verde 18.1
## 33 Central African Republic 10.5
## 34 Chad 5.2
## 35 Chile 15.0
## 36 China 21.3
## 37 Colombia 8.4
## 38 Comoros 3.0
## 39 Congo Brazzaville NA
## 40 Congo Kinshasa NA
## 41 Costa Rica 36.8
## 42 Cote d'Ivoire 8.9
## 43 Croatia 20.9
## 44 Cuba 43.2
## 45 Cyprus 14.3
## 46 Czech Republic 15.5
## 47 Denmark 38.0
## 48 Djibouti 13.8
## 49 Dominica 18.8
## 50 Dominican Rep 19.7
## 51 Ecuador 32.3
## 52 Egypt 1.8
## 53 El Salvador 19.0
## 54 Equatorial Guinea 10.0
## 55 Eritrea 22.0
## 56 Estonia 20.8
## 57 Ethiopia 21.9
## 58 Fiji NA
## 59 Finland 41.5
## 60 France 18.2
## 61 Gabon 16.7
## 62 Gambia 9.4
## 63 Georgia 5.1
## 64 Germany 32.8
## 65 Ghana 8.3
## 66 Greece 14.7
## 67 Grenada 13.3
## 68 Guatemala 12.0
## 69 Guinea-Bissau 10.0
## 70 Guinea NA
## 71 Guyana 30.0
## 72 Haiti 4.1
## 73 Honduras 23.4
## 74 Hungary 11.1
## 75 Iceland 42.9
## 76 India 10.7
## 77 Indonesia 18.2
## 78 Iran 2.8
## 79 Iraq 25.5
## 80 Ireland 13.3
## 81 Israel 17.5
## 82 Italy 21.3
## 83 Jamaica 13.3
## 84 Japan 11.3
## 85 Jordan 6.4
## 86 Kazakhstan 15.9
## 87 Kenya 9.8
## 88 Kiribati 4.3
## 89 Korea North 15.6
## 90 Korea South 13.7
## 91 Kuwait 7.7
## 92 Kyrgyzstan 25.6
## 93 Laos 25.2
## 94 Latvia 20.0
## 95 Lebanon 3.1
## 96 Lesotho 25.0
## 97 Liberia 12.5
## 98 Libya 7.7
## 99 Liechtenstein 24.0
## 100 Lithuania 17.7
## 101 Luxembourg 20.0
## 102 Macedonia 28.3
## 103 Madagascar NA
## 104 Malawi 20.8
## 105 Malaysia 10.8
## 106 Maldives 6.5
## 107 Mali 10.2
## 108 Malta 8.7
## 109 Marshall Islands 3.0
## 110 Mauritania 22.1
## 111 Mauritius 17.1
## 112 Mexico 28.2
## 113 Micronesia, Fed Stat 0.0
## 114 Moldova NA
## 115 Monaco 25.0
## 116 Mongolia 4.0
## 117 Morocco 10.5
## 118 Mozambique 34.8
## 119 Myanmar (Burma) NA
## 120 Namibia 26.9
## 121 Nauru 0.0
## 122 Nepal 33.2
## 123 Netherlands 41.3
## 124 New Zealand 33.6
## 125 Nicaragua 18.5
## 126 Niger 12.4
## 127 Nigeria 7.0
## 128 Norway 38.2
## 129 Oman 0.0
## 130 Pakistan 22.5
## 131 Palau 0.0
## 132 Panama 8.5
## 133 Papua New Guinea 0.9
## 134 Paraguay 12.5
## 135 Peru 27.5
## 136 Philippines 20.5
## 137 Poland 20.2
## 138 Portugal 19.5
## 139 Qatar 0.0
## 140 Romania 11.4
## 141 Russia 14.0
## 142 Rwanda 56.3
## 143 San Marino 15.0
## 144 Sao Tome 7.3
## 145 Saudi Arabia 0.0
## 146 Senegal 22.0
## 147 Seychelles 23.5
## 148 Sierra Leone 13.2
## 149 Singapore 24.5
## 150 Slovakia 19.3
## 151 Slovenia 13.3
## 152 Solomon Islands 0.0
## 153 Somalia 6.1
## 154 South Africa 44.5
## 155 Spain 36.3
## 156 Sri Lanka 5.8
## 157 St. Kitts & Nevis 6.7
## 158 St. Lucia 11.1
## 159 St. Vincent & Grenadine 18.2
## 160 Sudan 18.1
## 161 Suriname 25.5
## 162 Swaziland 13.6
## 163 Sweden 47.0
## 164 Switzerland 28.5
## 165 Syria 12.4
## 166 Taiwan NA
## 167 Tajikistan 17.5
## 168 Tanzania 30.4
## 169 Thailand 11.7
## 170 Togo 11.1
## 171 Tonga 3.1
## 172 Trinidad 26.8
## 173 Tunisia 22.8
## 174 Turkey 9.1
## 175 Turkmenistan 16.8
## 176 Tuvalu 0.0
## 177 UAE 22.5
## 178 Uganda 30.7
## 179 Ukraine 8.2
## 180 United Kingdom 19.5
## 181 United States 16.8
## 182 Uruguay 12.1
## 183 Uzbekistan 17.5
## 184 Vanuatu 3.8
## 185 Venezuela 18.6
## 186 Vietnam 25.8
## 187 Western Samoa NA
## 188 Yemen 0.3
## 189 Serbia & Montenegro NA
## 190 Zambia 15.2
## 191 Zimbabwe 15.2
Look at the values for Serbia & Montenegro (third from the bottom), which says NA. NA stantds for Not Available, meaning that the creator of this data set could not find a value of this variable for this observation. We can also see that other countries, such as Western Samoa, Taiwan, Myanmar (Burma), Moldova, etc., also have NA. There are as many as 11 observations where women09 is missing, as we see from the output of summary:
summary(world.data $ women09)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.00 9.70 15.55 17.18 22.95 56.30 11
When a variable contains a missing value, we have to tell R to ignore them when using functions such as the mean and median functions. That way, R will report the mean value of the variable excluding the observations with missing values.
To do so, we use the na.rm option, short for NA R(e)M(ove), as follows:
mean(world.data $ women09, na.rm = TRUE)
## [1] 17.17722
median(world.data $ women09, na.rm = TRUE)
## [1] 15.55
To summarize the dispersion of a numerical variable, we calculate standard deviation and variance (in addition to the range and IQR we have alreadycalculated using the summary function).
The sd function calculates the standard deviation, and the var function calculates the variance (square of the standard deviation).
sd(world.data $ women09, na.rm = TRUE)
## [1] 11.05299
var(world.data $ women09, na.rm = TRUE)
## [1] 122.1687
The standard deviation is about 11. This means that the values are away from the mean by about +11 or -11, on average. (Some values are away from the mean by more than +11 or less than -11, but if we take the average distance it’s plus or minus 11).
So, to report the summary of this variable, we calculate mean, median, the standard deviation, and the five number summary, instead of reporting all the actual values for each country. These numbers collectively describe the distribution of a numerical variable.
summary(world.data $ women09)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.00 9.70 15.55 17.18 22.95 56.30 11
sd(world.data $ women09, na.rm = TRUE)
## [1] 11.05299
Mean is about 17 and the standard deviation is about 11. The minimum is 0 and the maximum is 56.
Compare these with another variable women05, which measures the same concept but the variable was recorded in the year 2005.
# Data from 2009
summary(world.data $ women09)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.00 9.70 15.55 17.18 22.95 56.30 11
sd(world.data $ women09, na.rm = TRUE)
## [1] 11.05299
# Data from 2005
summary(world.data $ women05)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.00 8.25 13.00 15.38 20.45 45.30 80
sd(world.data $ women05, na.rm = TRUE)
## [1] 10.06678
Comparing the scores between 2005 and 2009, can we say that the countries have improved upon female representation during these four years. The mean, median, and maximum are all higher for 2009 than for 2005. We can also see that the standard deviation is also (slightly) greater for 2009, meaning that the values are more spread out in 2009. A part of the reason why this is the case is that we have more observations for 2009. For 2005, we have as many as 80 missing values, meaning that we only have 191-80 = 111 countries for 2005 whereas we have 191-11 = 180 countries for 2009.
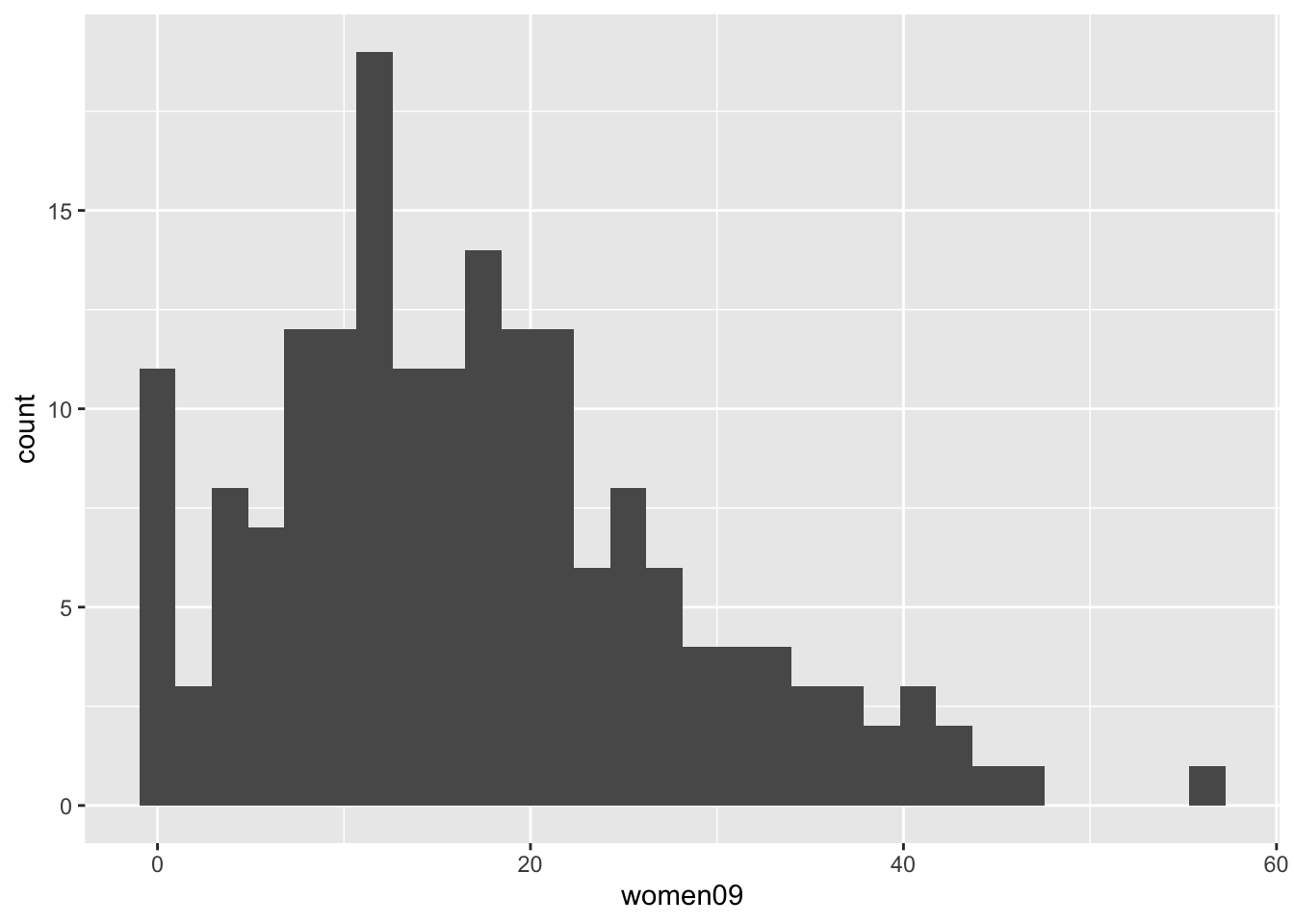
Another way of summarizing the information contained in numerical variables is to visualize the distribution of the variables. Histogram is one of the most commonly used graphical tool to summarize the central tendency and dispersion of numerical variables.
To draw a histogram using the ggplot function, we write:
ggplot(world.data, aes(x = women09)) + geom_histogram()
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 11 rows containing non-finite outside the scale range
## (`stat_bin()`).
ggplot(world.data, aes(x = women09)) + geom_histogram(binwidth = 1)
## Warning: Removed 11 rows containing non-finite outside the scale range
## (`stat_bin()`).
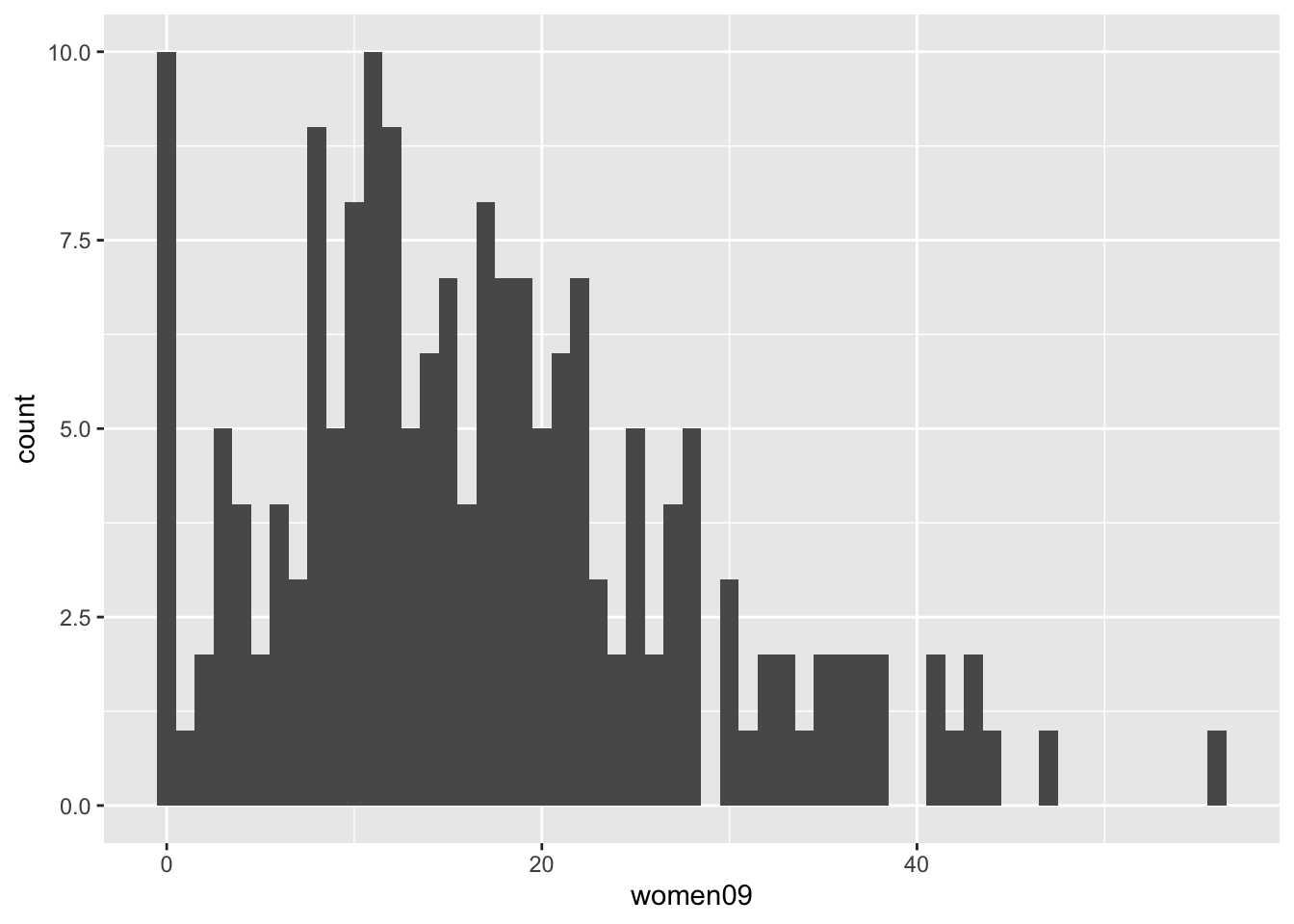
# Notice that we replace x = colony with x = women09
# and geom_bar() with geom_histogram()