Data management
Instructions
- Homework assignment is here with all questions commented out.
- Complete all of the coding tasks in the
.qmdfile - Upload your individual exercise to your
GitHubrepo by Wed 11:59pm. - Remember to clean your github repo and sort hw submissions by weeks. Each week should have one folder.
# Preparation -------------------------------------------------------------
rm(list = ls()) # delete everything in the memory
library(ggplot2) # for graphics
library(Hmisc) # for rcorr
##
## Attaching package: 'Hmisc'
## The following objects are masked from 'package:base':
##
## format.pval, units
library(stargazer) # Regression table
##
## Please cite as:
## Hlavac, Marek (2022). stargazer: Well-Formatted Regression and Summary Statistics Tables.
## R package version 5.2.3. https://CRAN.R-project.org/package=stargazer
library(effects) # for effect
## Loading required package: carData
## lattice theme set by effectsTheme()
## See ?effectsTheme for details.
# Read-in the world data
world.data <- read.csv("world.csv")
# Task 1 ------------------------------------------------------------------
# Examine the data
#---------------------------------------
# Describe Y
#---------------------------------------
# Numerical summary
summary(world.data $ women09)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.00 9.70 15.55 17.18 22.95 56.30 11
# Graphical summary
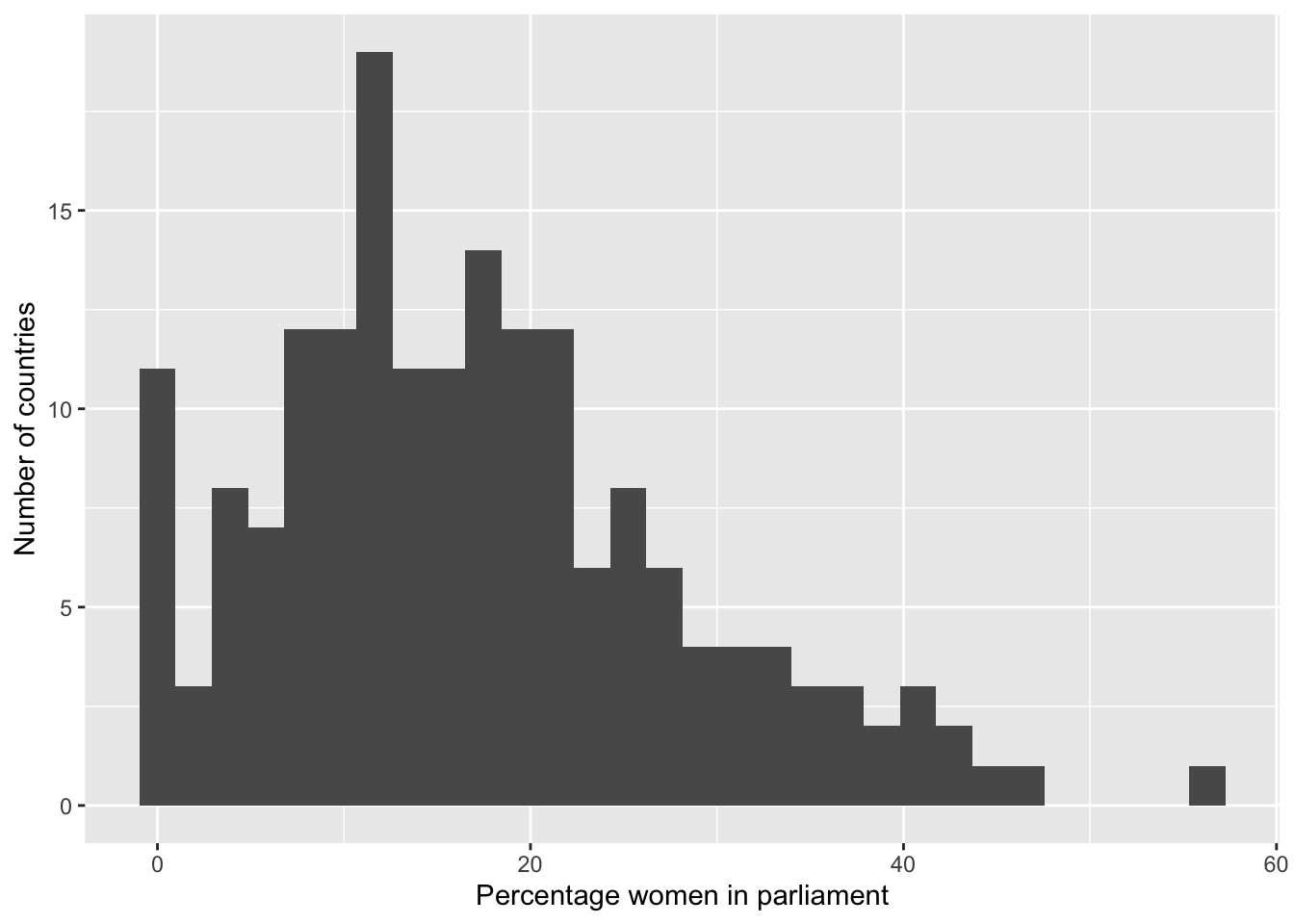
g <- ggplot( world.data, aes( x = women09 ) ) + geom_histogram()
g <- g + ylab("Number of countries") + xlab("Percentage women in parliament")
g
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 11 rows containing non-finite outside the scale range
## (`stat_bin()`).
#---------------------------------------
# Describe X: per capita GDP
#---------------------------------------
# Numerical summary
summary(world.data $ gdp_10_thou)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.0090 0.0503 0.1897 0.6018 0.6320 4.7354 14
# Graphical summary
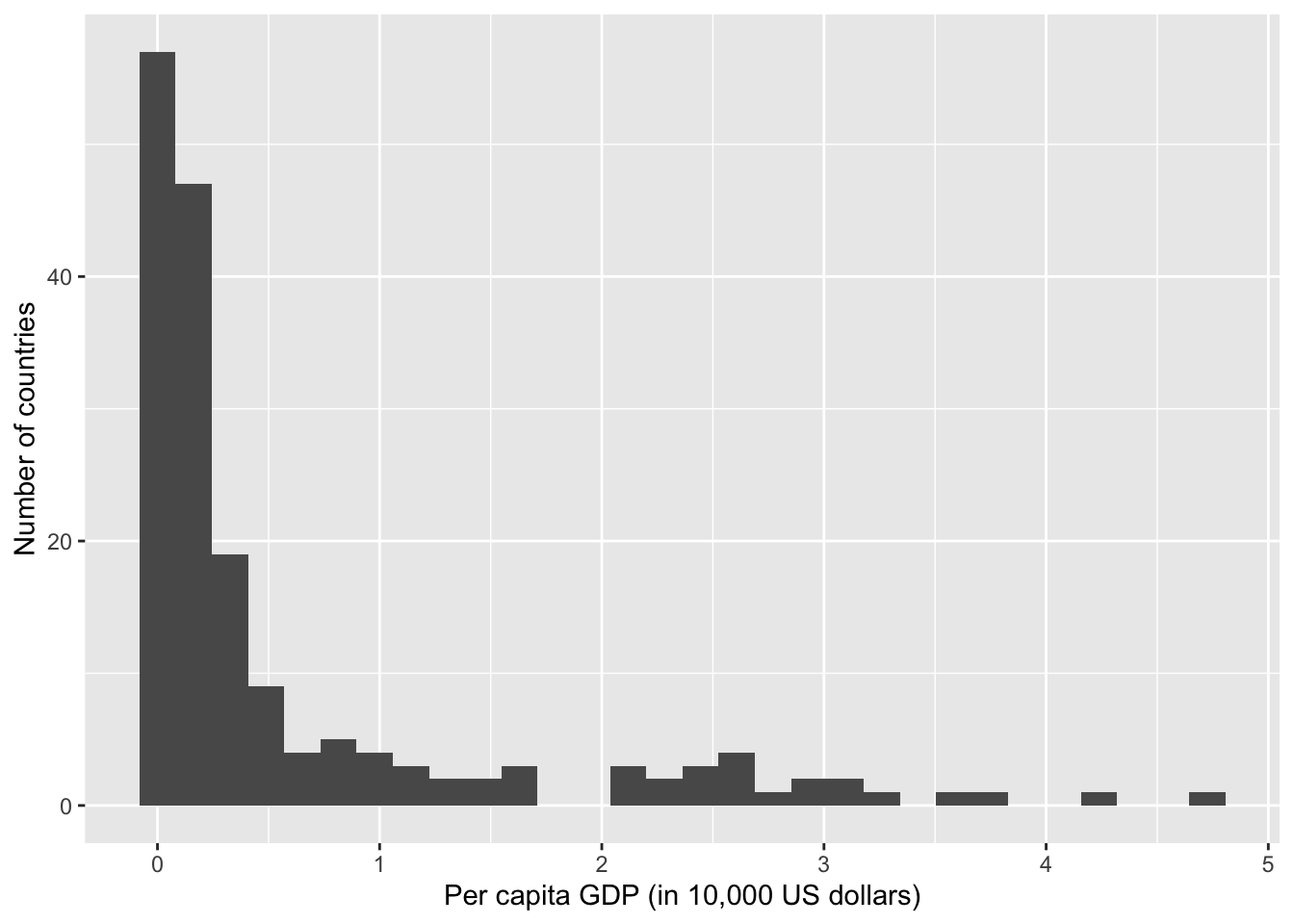
g <- ggplot( world.data, aes( x = gdp_10_thou ) ) + geom_histogram()
g <- g + ylab("Number of countries") + xlab("Per capita GDP (in 10,000 US dollars)")
g
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 14 rows containing non-finite outside the scale range
## (`stat_bin()`).
#---------------------------------------
# Describe X-Y
#---------------------------------------
# To describe an X-Y relationship graphically, we draw what's called a
# scatterplot that shows the values of the X variable on the X-axis and
# the values of the Y variable on the Y-axis for all observations.
# To create a scatterplot, we use the geom_point function (because
# each observation is denoted by a point.)
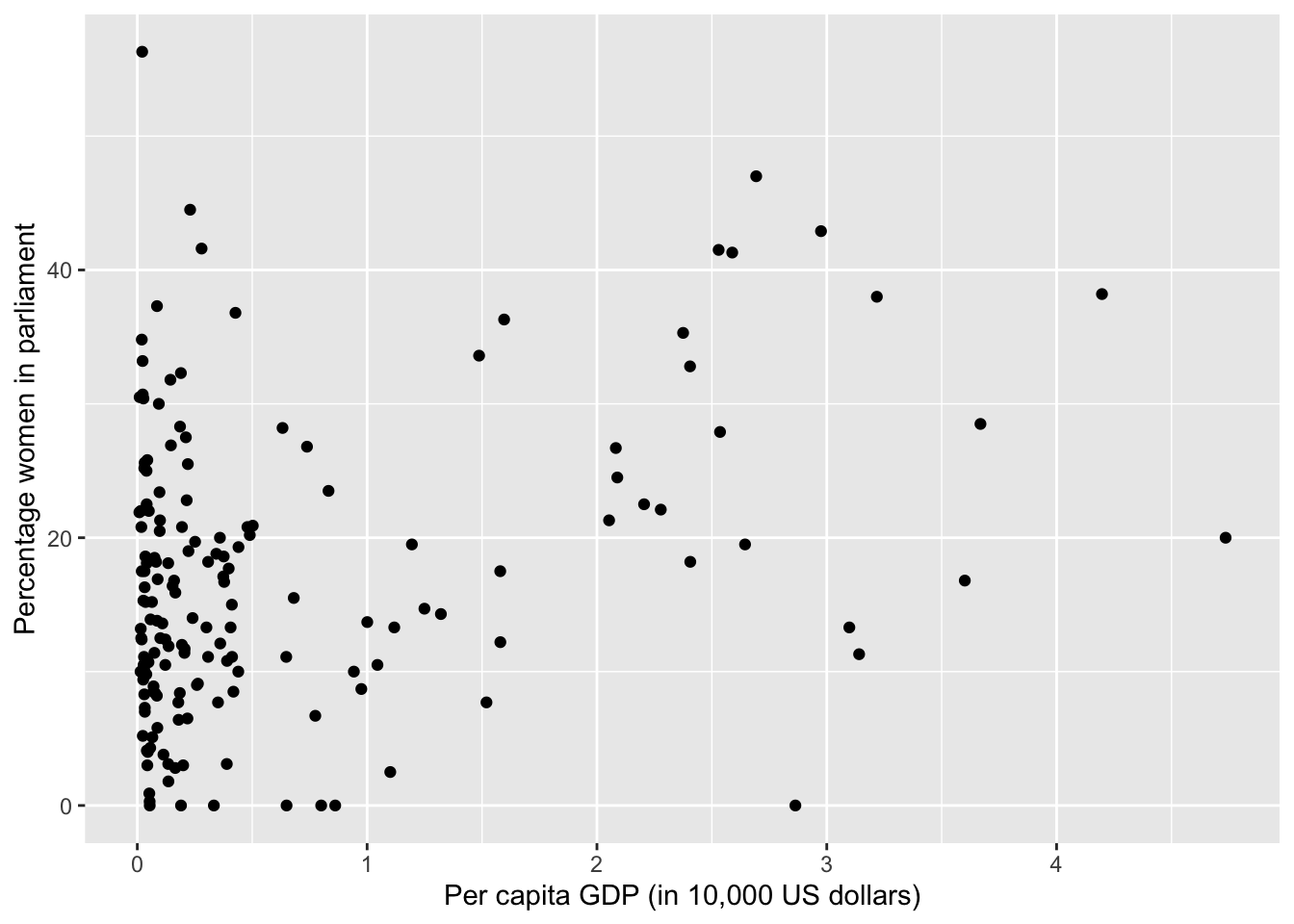
g <- ggplot(world.data, aes( x = gdp_10_thou, y = women09) ) + geom_point()
g <- g + ylab("Percentage women in parliament") + xlab("Per capita GDP (in 10,000 US dollars)")
g
## Warning: Removed 22 rows containing missing values or values outside the scale range
## (`geom_point()`).
# Task 2 ------------------------------------------------------------------
# Omit observations with NAs
women.gdp <- world.data[is.na(world.data $ women09) == FALSE & is.na(world.data $ gdp_10_thou) == FALSE, ]
dim(women.gdp)
## [1] 169 62
# Task 3 ------------------------------------------------------------------
# Calculate test-statistic & p-value
# The test statistic for a bivariate test of two numerical variables is
# (Pearson's) correlation coefficient.
# To calculate correlation coefficient (r), we first need to create a matrix object
# using the as.matrix function.
women.gdp.mat <- as.matrix(women.gdp[ c("gdp_10_thou","women09")])
# Then we use the rcorr function available in the Hmisc package.
rcorr(women.gdp.mat, type = "pearson")
## gdp_10_thou women09
## gdp_10_thou 1.00 0.31
## women09 0.31 1.00
##
## n= 169
##
##
## P
## gdp_10_thou women09
## gdp_10_thou 0
## women09 0
# The correlation coefficient is 0.31 with the p-value < 0.001.
# The relationship is positive and highly statistically significant.
# Task 4 ------------------------------------------------------------------
# H0: the effect of gdp_10_thou on women09 is zero.
# Ha: the effect of gdp_10_thou on women09 is positive.
# Task 5 ------------------------------------------------------------------
# Regression
fit.wg <- lm(women09 ~ gdp_10_thou, data = women.gdp)
stargazer(fit.wg, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## gdp_10_thou 3.457***
## (0.835)
##
## Constant 14.843***
## (0.954)
##
## -----------------------------------------------
## Observations 169
## R2 0.093
## Adjusted R2 0.088
## Residual Std. Error 10.379 (df = 167)
## F Statistic 17.139*** (df = 1; 167)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
# (a)
# Regression equation: women09 = 14.843 + 3.457 * gdp_10_thou
# (b)
# Positive
# (c)
# An increase in per capita GDP (gdp_10_thou) by 10000 dollars will lead to an increase
# in female representation by 3.457 percentage points.
# An increase in per capita GDP (gdp_10_thou) by 1000 dollars will lead to an increase
# in female representation by 0.3457 percentage points.
# (d)
# The estimated coefficient for gdp_10_thou is highly statistically significant.
# We can reject the null hypothesis at 1% significance level.
# Task 6 ------------------------------------------------------------------
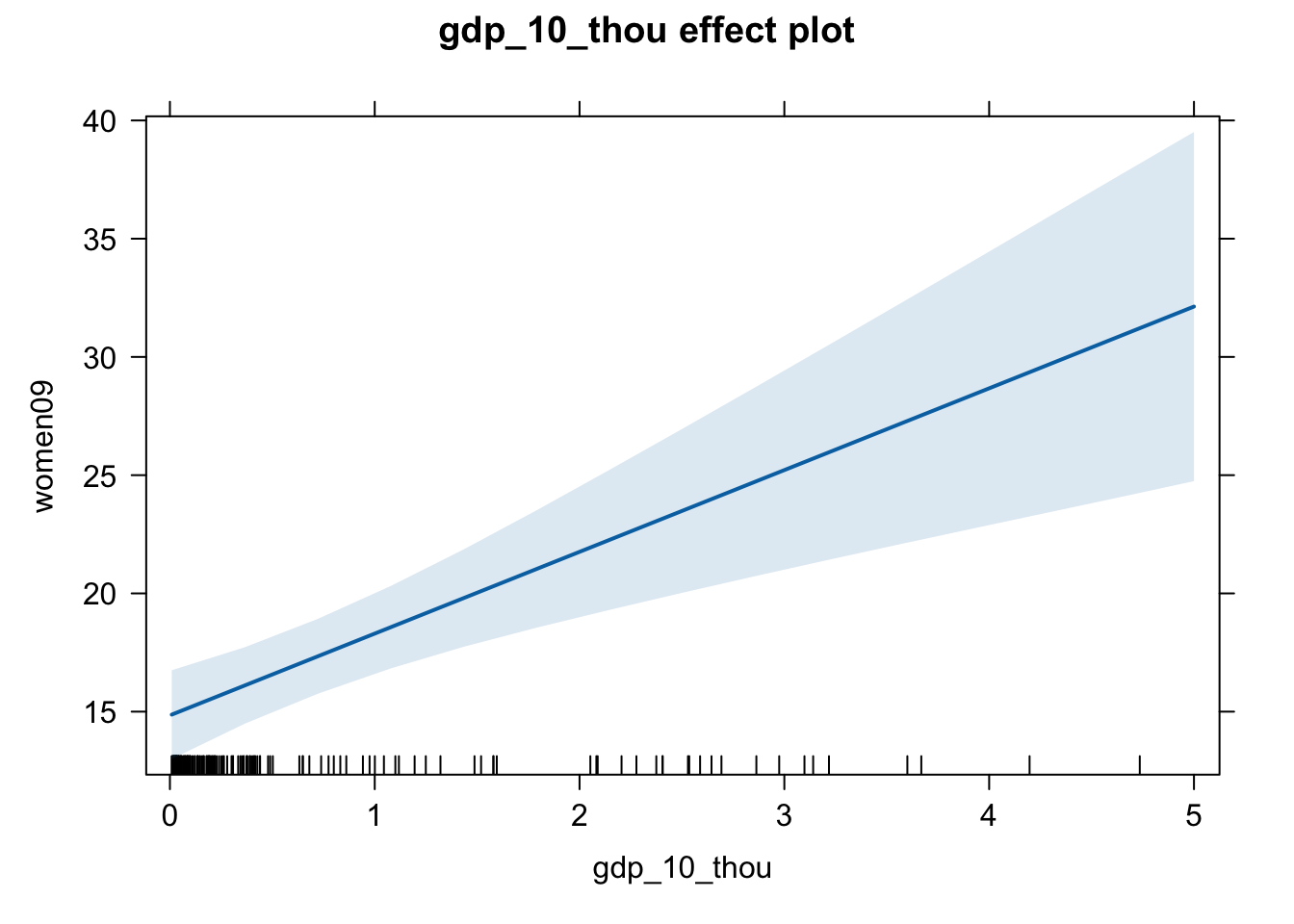
eff.wg <- effect(term = "gdp_10_thou", mod = fit.wg)
plot(eff.wg)
# Task 7 ------------------------------------------------------------------
stargazer(fit.wg, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## gdp_10_thou 3.457***
## (0.835)
##
## Constant 14.843***
## (0.954)
##
## -----------------------------------------------
## Observations 169
## R2 0.093
## Adjusted R2 0.088
## Residual Std. Error 10.379 (df = 167)
## F Statistic 17.139*** (df = 1; 167)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
# (a)
# The R-squared is 0.093, which means that about 9% of the total variation in
# Female Representation is explained by per capita GDP.
# Many factors could potentially influence the variation in female representation
# across countries, and economic development appears to be one of them.
# R-squred of 9 % seems rather small, and it implies that either our model ignores
# some other important determinants, or the variation in female representation
# is quite random.
# (b)
# The Residual Std. Error is 10.379. That is, our predictions are off by about
# 10 percentage points, on average. I would say that this is rather big.
# Again, this implies that either our model ignores some other important
# determinants, or the variation in female representation is quite random.
# Task 8 ------------------------------------------------------------------
# Predicted values
women.gdp $ y.hat <- predict(fit.wg)
# Values for Rwanda
women.gdp[ women.gdp $ country == "Rwanda", c("women09", "y.hat") ]
## women09 y.hat
## 142 56.3 14.91632
# The predicted value of Female Representation for Rwanda is 14.91%, whereas
# the actual value is 56.3%. I would say that our prediction is very, very far off.
# Task 9 ------------------------------------------------------------------
# Do the analyses for PR and non-PR countries seperately to control for
# electoral system "manually".
# Re-label the PR variable
women.gdp $ pr <- factor(women.gdp $ pr_sys, levels = c("No", "Yes"), labels = c("Non-PR", "PR"))
# Make sure it worked
table(women.gdp $ pr_sys, women.gdp $ pr)
##
## Non-PR PR
## No 106 0
## Yes 0 63
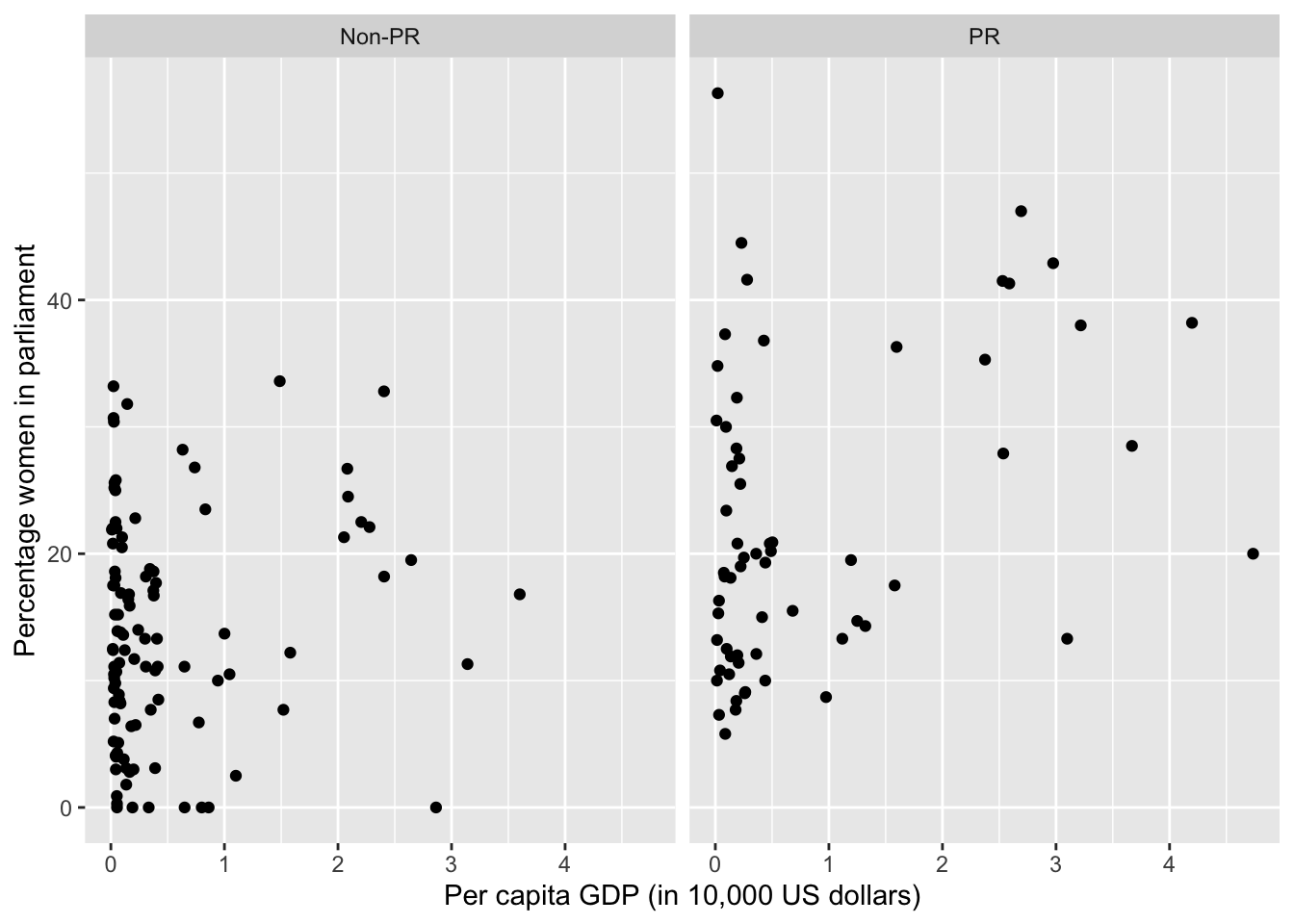
# Examine the X-Y relationship graphically
g <- ggplot(women.gdp, aes( x = gdp_10_thou, y = women09) ) + geom_point()
g <- g + ylab("Percentage women in parliament") + xlab("Per capita GDP (in 10,000 US dollars)")
g <- g + facet_grid( ~ pr)
g
# Create data sets for PR and non-PR
women.gdp.pr <- women.gdp[women.gdp $ pr == "PR", ]
women.gdp.mj <- women.gdp[women.gdp $ pr == "Non-PR", ]
# Separate regression models for PR and non-PR
fit.wg.pr <- lm(women09 ~ gdp_10_thou, data = women.gdp.pr)
fit.wg.mj <- lm(women09 ~ gdp_10_thou, data = women.gdp.mj)
stargazer(fit.wg.pr, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## gdp_10_thou 3.641***
## (1.218)
##
## Constant 19.375***
## (1.748)
##
## -----------------------------------------------
## Observations 63
## R2 0.128
## Adjusted R2 0.113
## Residual Std. Error 11.254 (df = 61)
## F Statistic 8.935*** (df = 1; 61)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
stargazer(fit.wg.mj, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## gdp_10_thou 1.655
## (1.081)
##
## Constant 12.956***
## (1.001)
##
## -----------------------------------------------
## Observations 106
## R2 0.022
## Adjusted R2 0.013
## Residual Std. Error 8.685 (df = 104)
## F Statistic 2.343 (df = 1; 104)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
# Alternatively, we can have one table that summarizes two (or more)
# regression models, as follows:
stargazer(fit.wg.pr, fit.wg.mj, type = "text")
##
## =============================================================
## Dependent variable:
## -----------------------------------------
## women09
## (1) (2)
## -------------------------------------------------------------
## gdp_10_thou 3.641*** 1.655
## (1.218) (1.081)
##
## Constant 19.375*** 12.956***
## (1.748) (1.001)
##
## -------------------------------------------------------------
## Observations 63 106
## R2 0.128 0.022
## Adjusted R2 0.113 0.013
## Residual Std. Error 11.254 (df = 61) 8.685 (df = 104)
## F Statistic 8.935*** (df = 1; 61) 2.343 (df = 1; 104)
## =============================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
# Task 10 -----------------------------------------------------------------
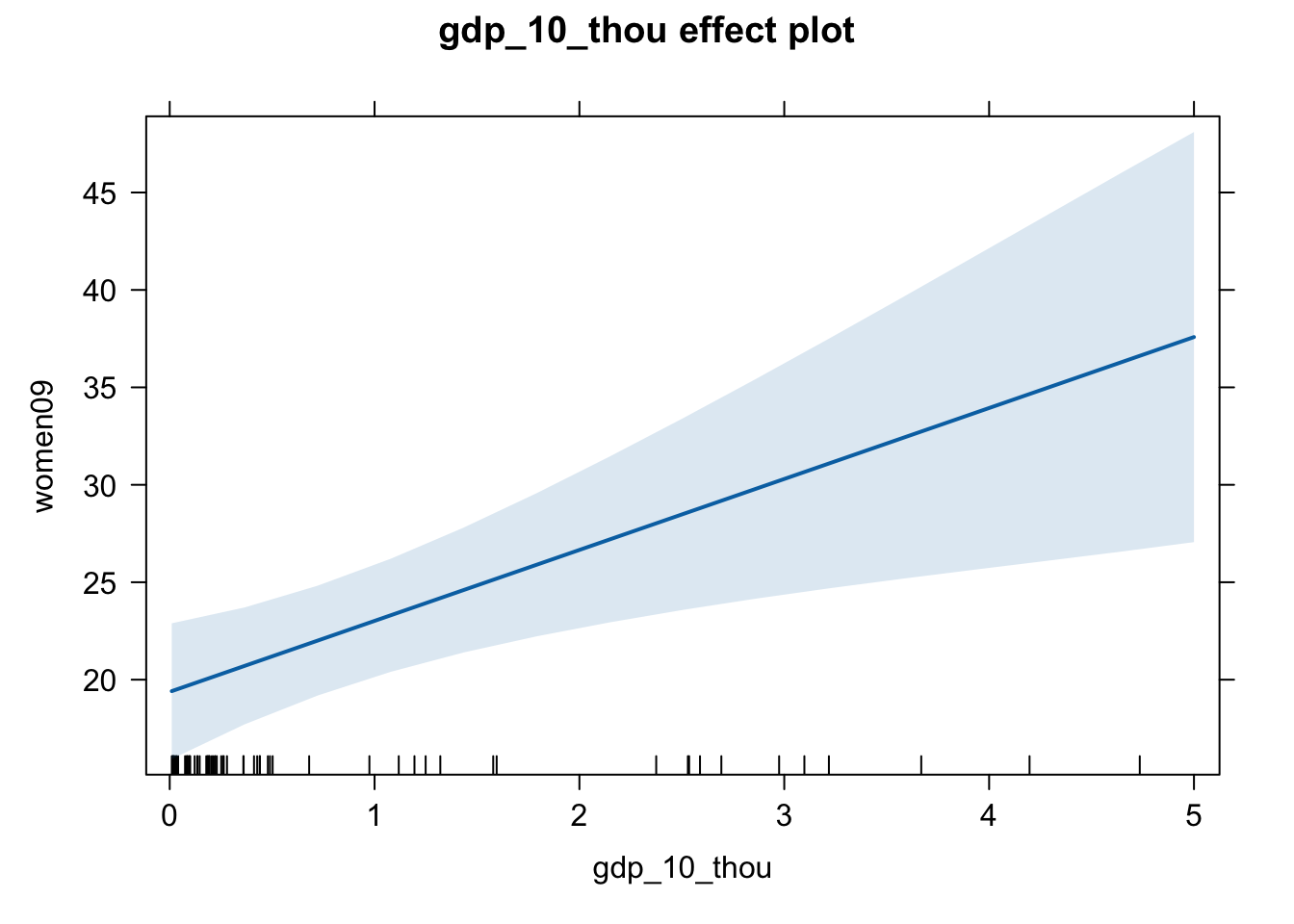
# The estimated effect of gdp_10_thou for PR countries.
# From the stargazer table above, we can see that the estimated effect of
# gdp_10_thou on women09 is positive (3.641) and statistically significant
# for PR countries (p < 0.01).
eff.wg.pr <- effect(term = "gdp_10_thou", mod = fit.wg.pr)
plot(eff.wg.pr)
# Task 11 -----------------------------------------------------------------
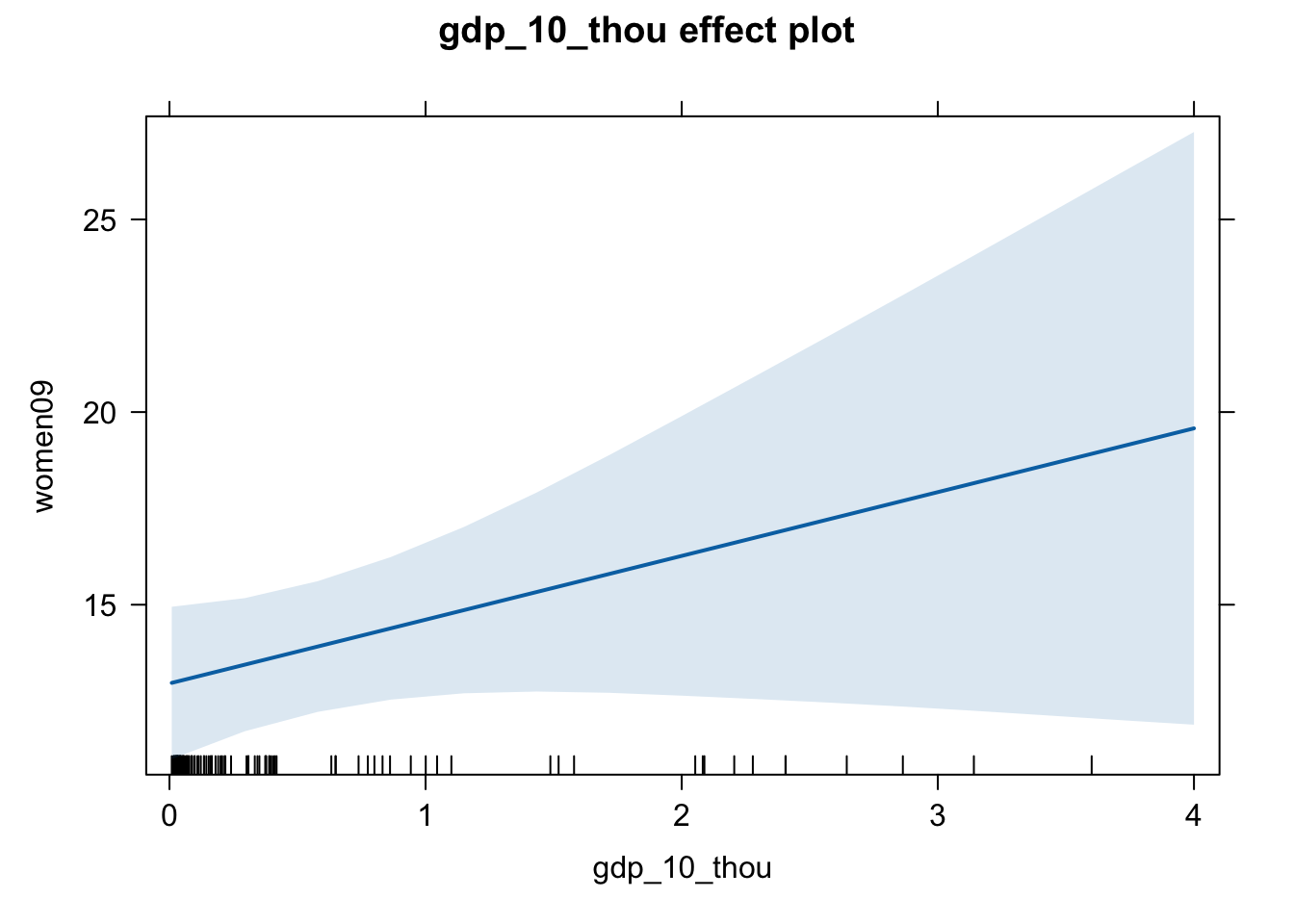
# The estimated effect of gdp_10_thou for non-PR countries.
# From the stargazer table above, we can see that the estimated effect of
# gdp_10_thou on women09 is positive (1.655) but not statistically significant.
# That is, we cannot reject the null hypothesis that the effect is zero.
eff.wg.mj <- effect(term = "gdp_10_thou", mod = fit.wg.mj)
plot(eff.wg.mj)
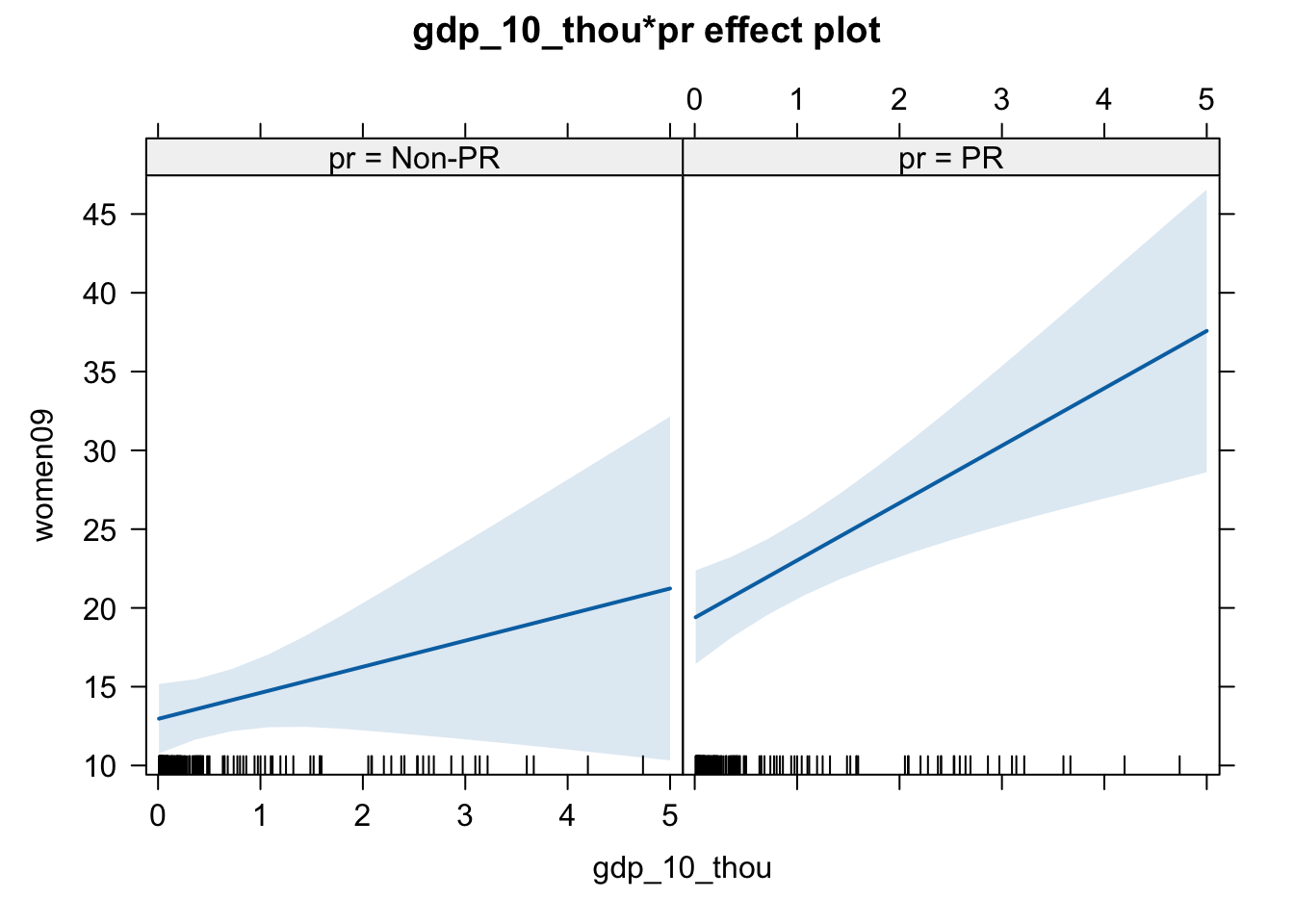
# Advanced: If you want to create a graph that shows the estimated effects
# of X on Y for two different scenarios (PR and non-PR), we can do the following.
# We will talk a lot more about this type of analyses in the Spring term.
fit.i <- lm(women09 ~ gdp_10_thou + pr + gdp_10_thou:pr, data = women.gdp)
eff.i <- effect(term = "gdp_10_thou:pr", mod = fit.i)
plot(eff.i)
# Task 12 -----------------------------------------------------------------
# Predicted values.
women.gdp.pr $ y.hat <- predict(fit.wg.pr)
# Values for Rwanda
women.gdp.pr[ women.gdp.pr $ country == "Rwanda", c("women09", "y.hat") ]
## women09 y.hat
## 142 56.3 19.45267