Multiple Regression
Instructions
- Homework assignment is here with all questions commented out.
- Complete all of the coding tasks in the
.qmdfile - Upload your individual exercise to your
GitHubrepo by Wed 11:59pm. - Remember to clean your github repo and sort hw submissions by weeks. Each week should have one folder.
Note: You can, and I will recommend to, convert all the graphs to prettier ones using ggplot() which you all learned before. I will spend time converting everything to ggplot next semester.
# Preparation -------------------------------------------------------------
rm(list = ls()) # delete everything in the memory
library(foreign) # for read.dta
library(ggplot2) # for graphics
library(stargazer) # Regression table
library(effects)
1. Estimate a constant-only model
path <- "/Users/howardliu/methodsPol/content/assignment/"
wd <- read.csv(paste0(path, "world.csv"))
fit.0 <- lm(women09 ~ 1, data = wd)
stargazer(fit.0, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## Constant 17.177***
## (0.824)
##
## -----------------------------------------------
## Observations 180
## R2 0.000
## Adjusted R2 0.000
## Residual Std. Error 11.053 (df = 179)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
2. Estimate a model that uses per capita GDP (gdp_10_thou) as the main independent variable.
fit.gdp <- lm(women09 ~ gdp_10_thou, data = wd)
stargazer(fit.0, fit.gdp, type = "text")
##
## =============================================================
## Dependent variable:
## -----------------------------------------
## women09
## (1) (2)
## -------------------------------------------------------------
## gdp_10_thou 3.457***
## (0.835)
##
## Constant 17.177*** 14.843***
## (0.824) (0.954)
##
## -------------------------------------------------------------
## Observations 180 169
## R2 0.000 0.093
## Adjusted R2 0.000 0.088
## Residual Std. Error 11.053 (df = 179) 10.379 (df = 167)
## F Statistic 17.139*** (df = 1; 167)
## =============================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
3. Create a graph that shows the estimated effect of per capita GDP on female representation using the effect function.
plot(effect(term = "gdp_10_thou", mod = fit.gdp))
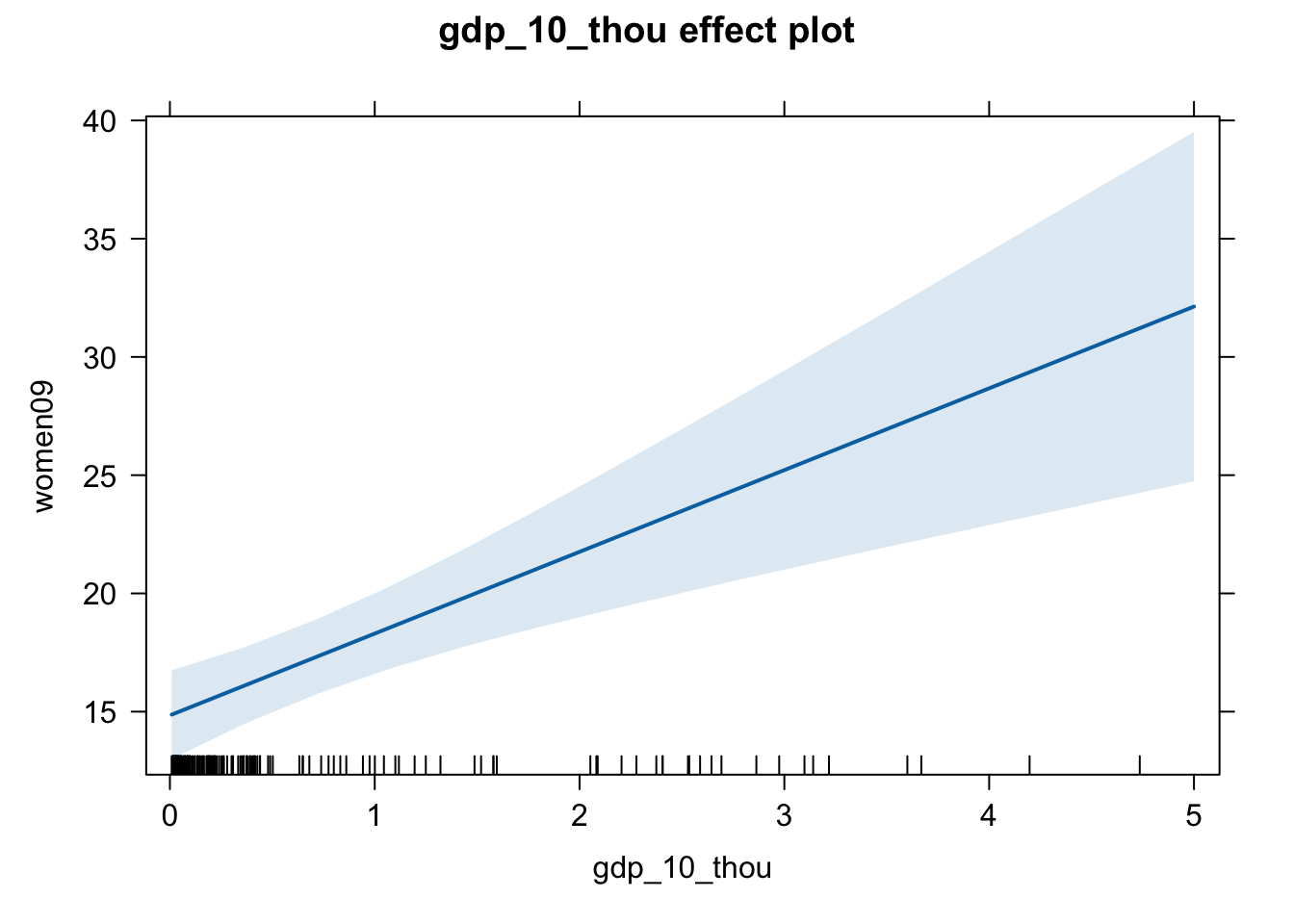
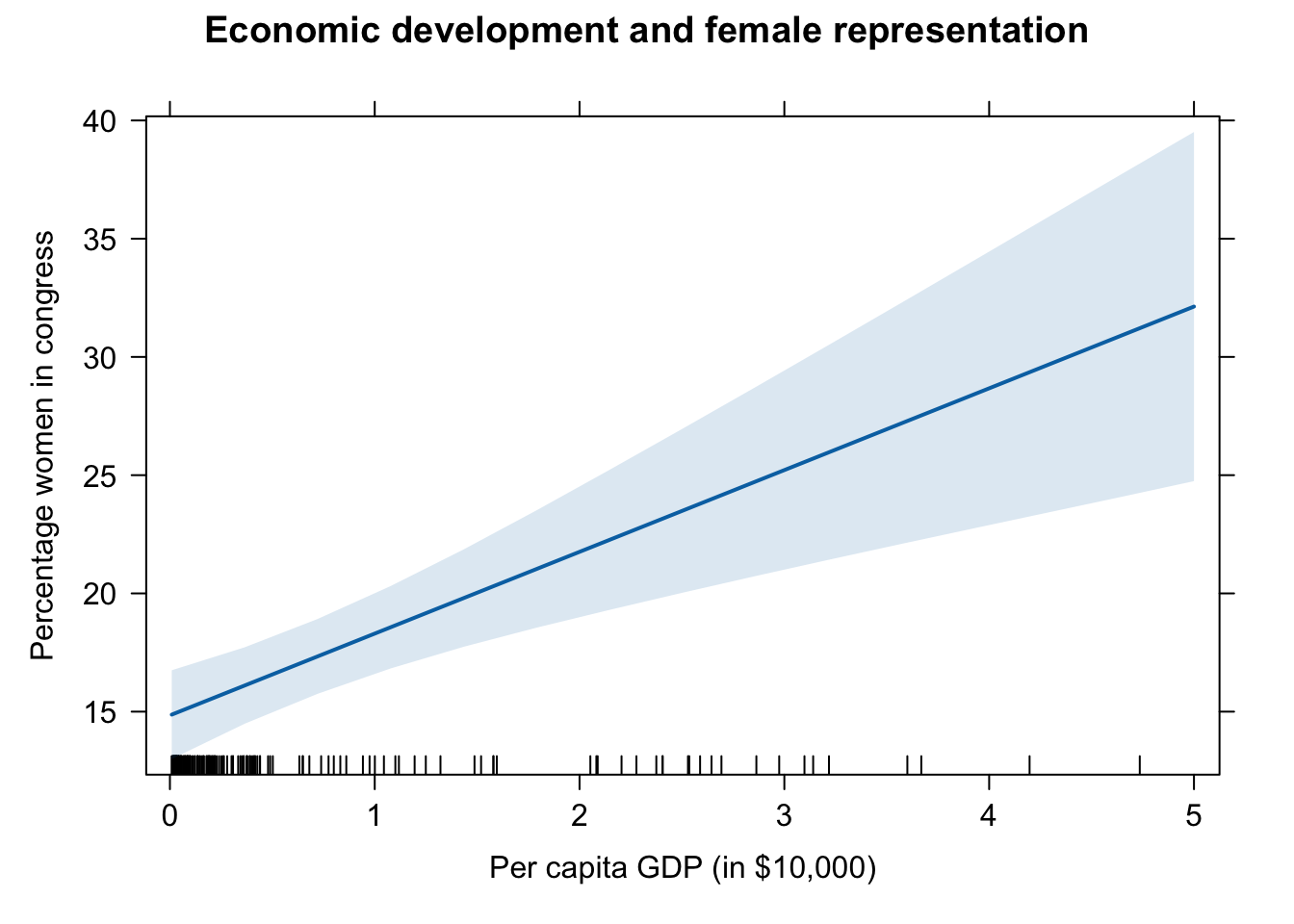
plot(effect(term = "gdp_10_thou", mod = fit.gdp),
main = "Economic development and female representation",
xlab = "Per capita GDP (in $10,000)",
ylab = "Percentage women in congress")
4. Estimate a model that uses a dummy variable that measures electoral system (pr_sys) as the main independent variable.
table(wd $ pr_sys)
##
## No Yes
## 124 67
fit.pr <- lm(women09 ~ pr_sys, data = wd)
stargazer(fit.pr, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## pr_sysYes 8.230***
## (1.600)
##
## Constant 14.160***
## (0.969)
##
## -----------------------------------------------
## Observations 180
## R2 0.129
## Adjusted R2 0.125
## Residual Std. Error 10.342 (df = 178)
## F Statistic 26.471*** (df = 1; 178)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
5. Create a graph that shows the estimated effect of electoral system on female representation using the effect function.
plot(effect(term = "pr_sys", mod = fit.pr))
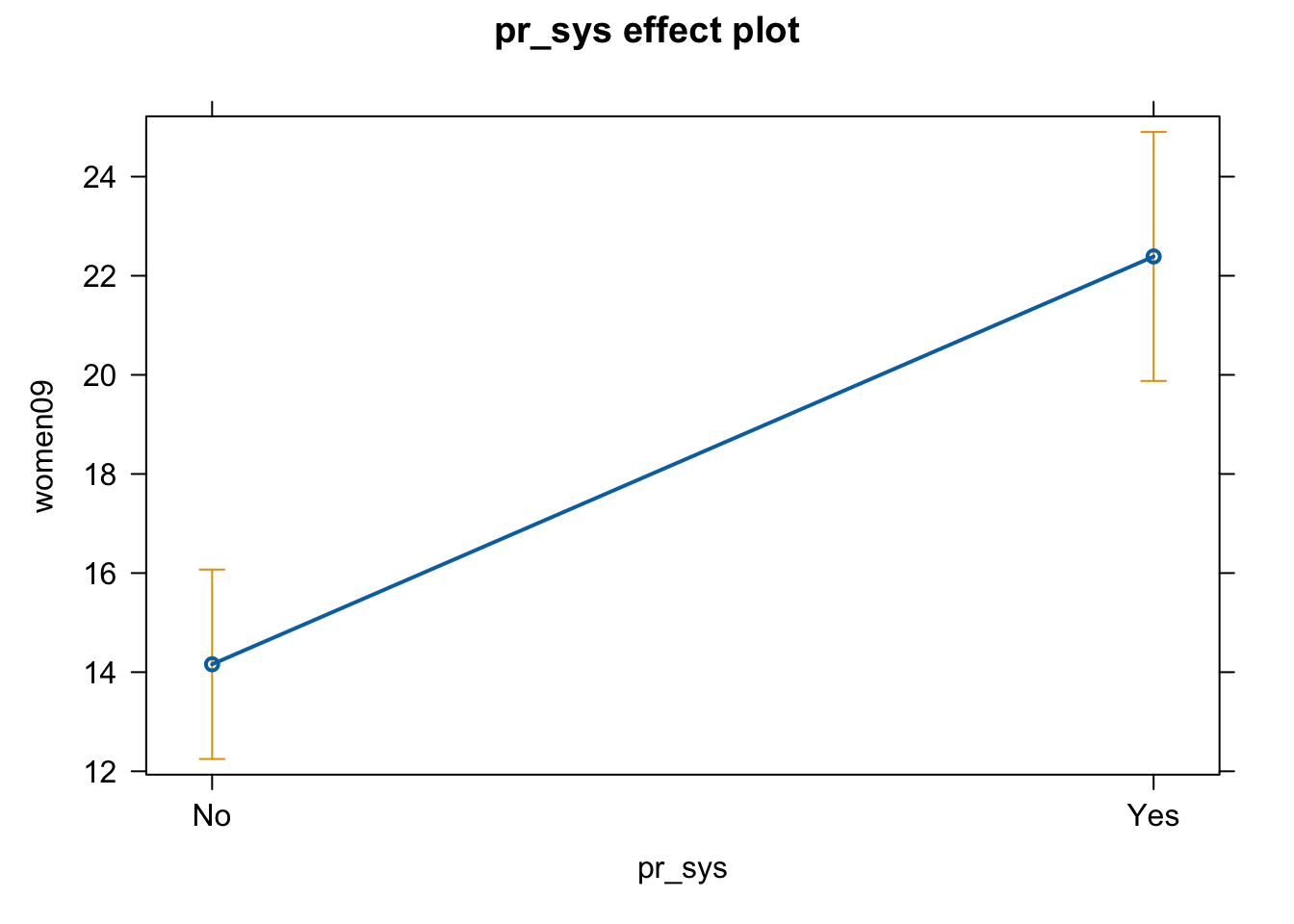
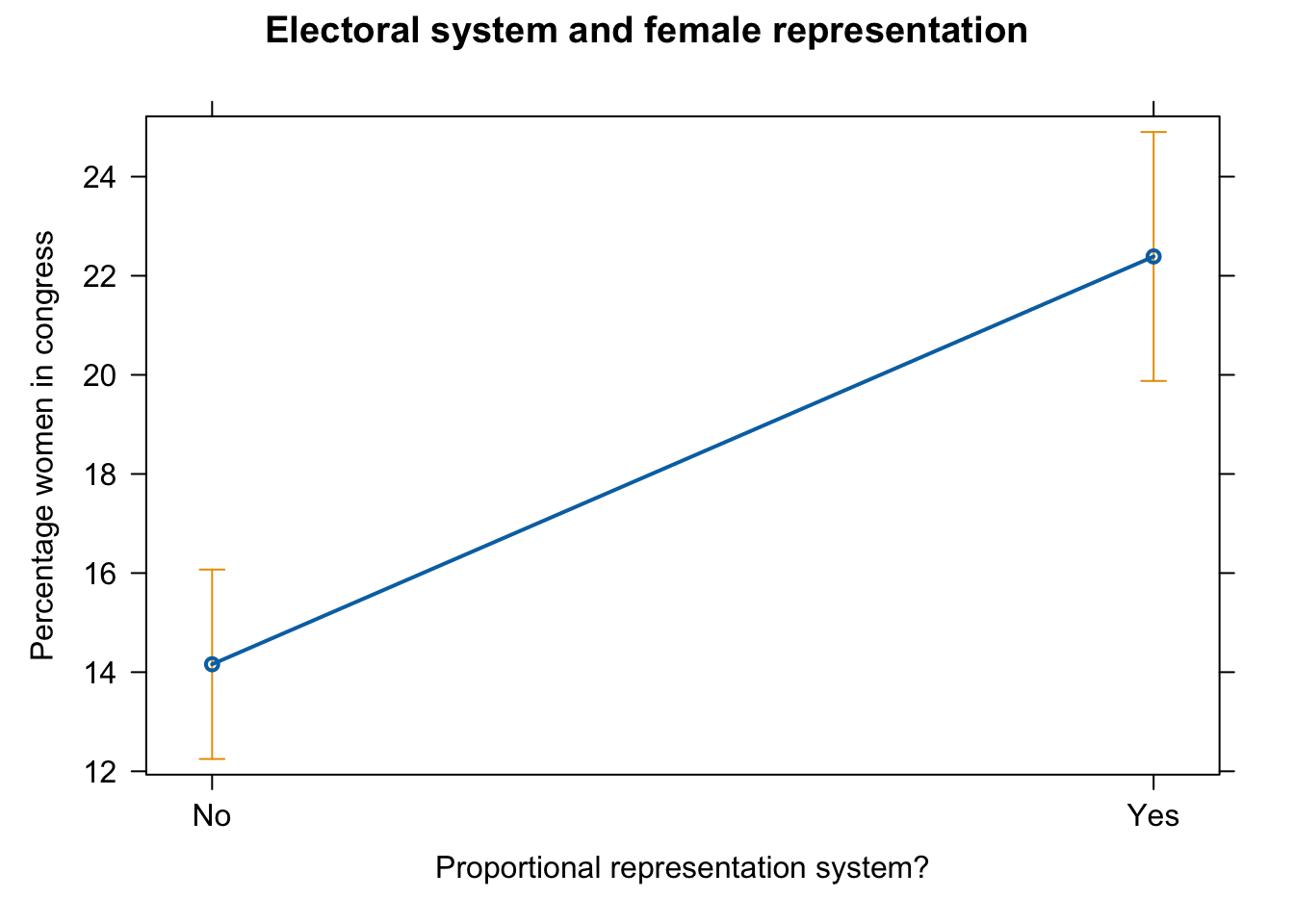
plot(effect(term = "pr_sys", mod = fit.pr),
main = "Electoral system and female representation",
xlab = "Proportional representation system?",
ylab = "Percentage women in congress")
6. Estimate a model that includes per capita GDP AND electoral system dummy at the same time.
fit.gdp.pr <- lm(women09 ~ gdp_10_thou + pr_sys, data = wd)
stargazer(fit.gdp.pr, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## gdp_10_thou 2.786***
## (0.795)
##
## pr_sysYes 7.701***
## (1.571)
##
## Constant 12.392***
## (1.025)
##
## -----------------------------------------------
## Observations 169
## R2 0.208
## Adjusted R2 0.198
## Residual Std. Error 9.730 (df = 166)
## F Statistic 21.760*** (df = 2; 166)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
7. Comparing the four models you have estimated so far, which one fit the data best?
stargazer(fit.0, fit.gdp, fit.pr, fit.gdp.pr, type = "text", omit.stat = "f")
##
## ==========================================================================================
## Dependent variable:
## ----------------------------------------------------------------------
## women09
## (1) (2) (3) (4)
## ------------------------------------------------------------------------------------------
## gdp_10_thou 3.457*** 2.786***
## (0.835) (0.795)
##
## pr_sysYes 8.230*** 7.701***
## (1.600) (1.571)
##
## Constant 17.177*** 14.843*** 14.160*** 12.392***
## (0.824) (0.954) (0.969) (1.025)
##
## ------------------------------------------------------------------------------------------
## Observations 180 169 180 169
## R2 0.000 0.093 0.129 0.208
## Adjusted R2 0.000 0.088 0.125 0.198
## Residual Std. Error 11.053 (df = 179) 10.379 (df = 167) 10.342 (df = 178) 9.730 (df = 166)
## ==========================================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
# The fourth model fits the data best.
8. Create a graph that shows the effect of per capita GDP on Y for countries that adopt proportional representation system.
# Hint 1: use the given.values option.
# Hint 2: to refer to the pr_sys variable in the given.values option,
# you need to call it "pr_sysYes", not "pr_sys".
# Hint 3: pr_sysYes is either 1 (Yes) or 0 (No)
plot(effect(term = "gdp_10_thou", mod = fit.gdp.pr,
given.values = c("pr_sysYes" = 1)))
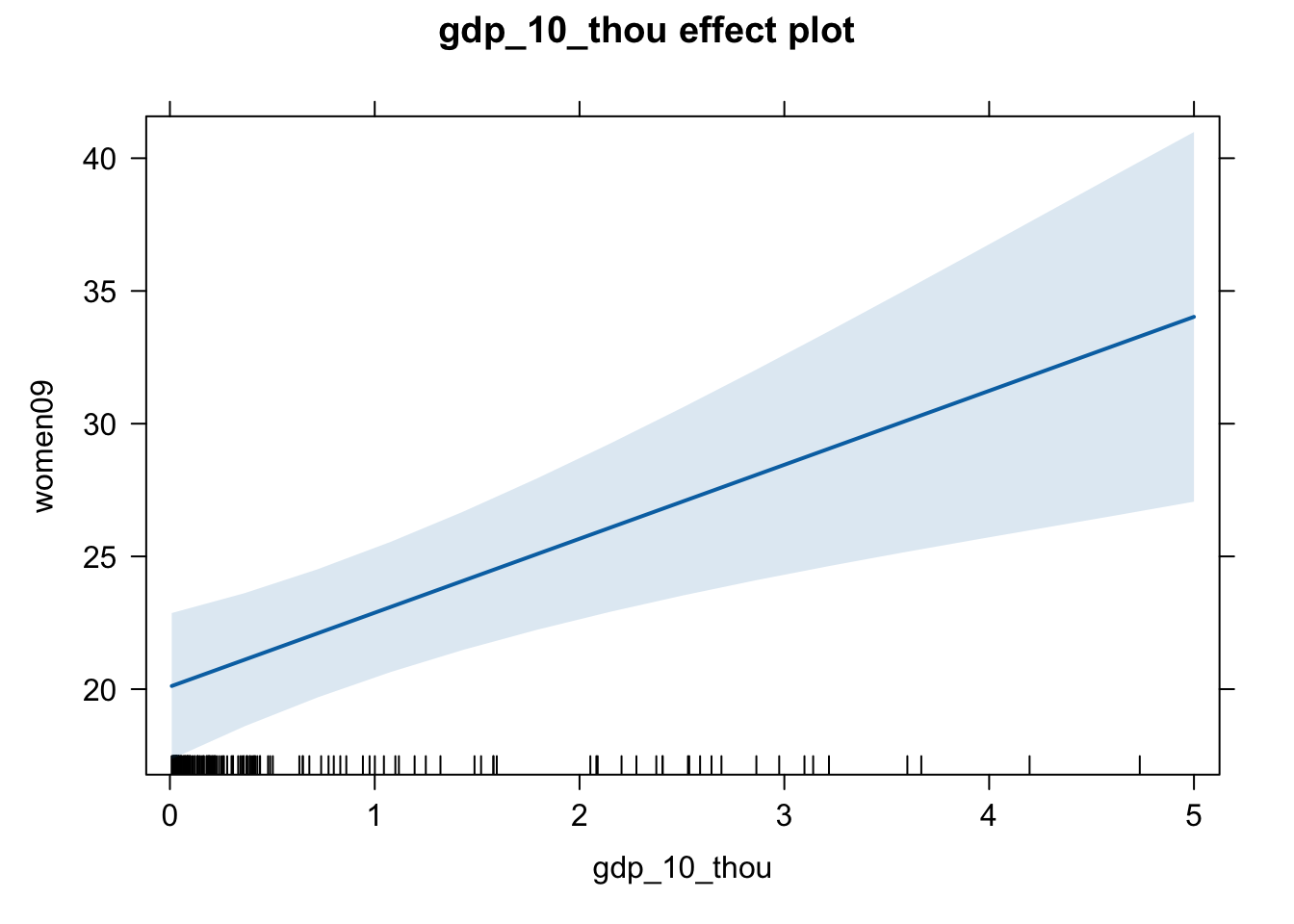
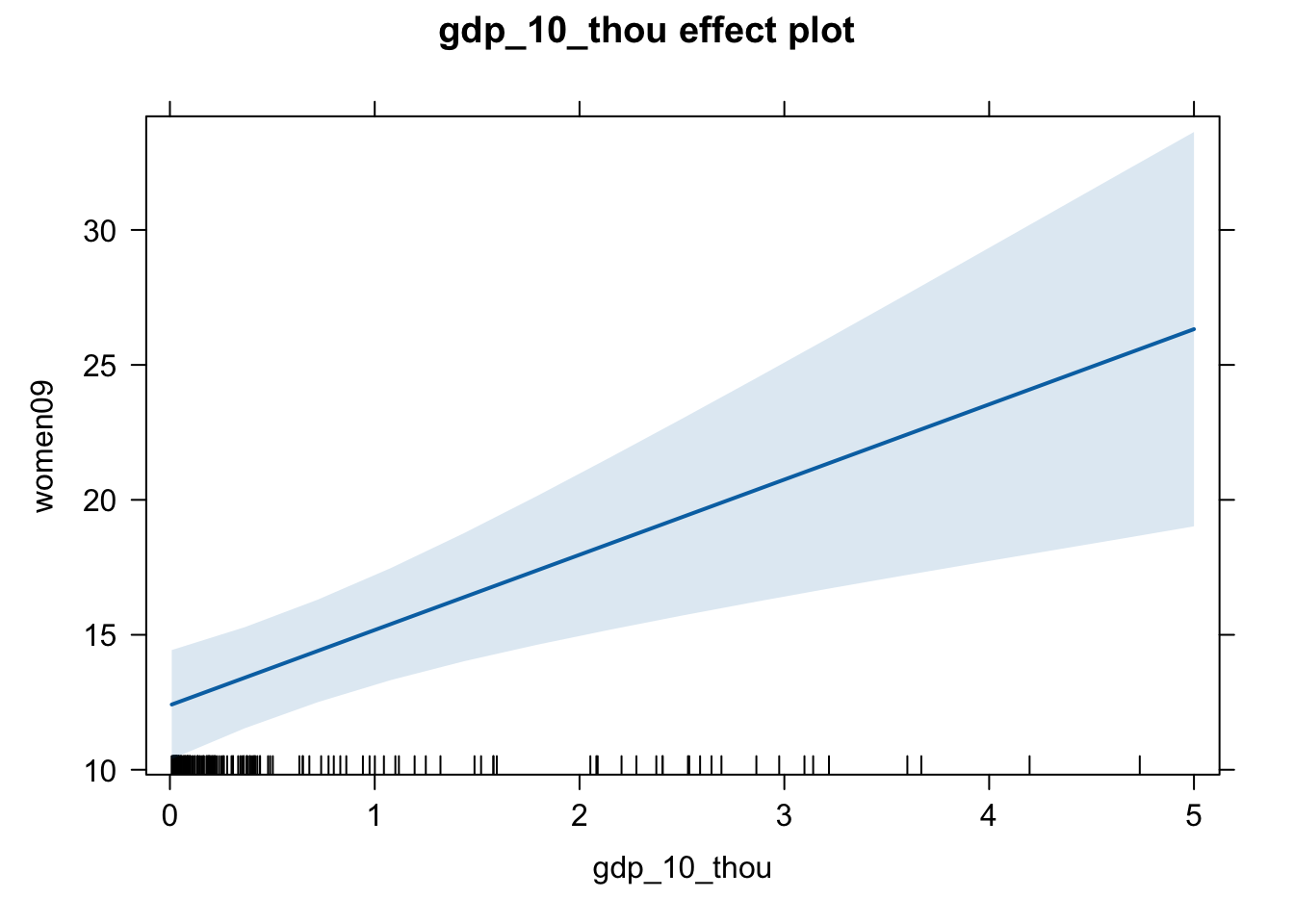
plot(effect(term = "gdp_10_thou", mod = fit.gdp.pr,
given.values = c("pr_sysYes" = 0)))
plot.gdp.pr1 <- plot(effect(term = "gdp_10_thou", mod = fit.gdp.pr,
given.values = c("pr_sysYes" = 1)), ylim = c(10,40))
plot.gdp.pr0 <- plot(effect(term = "gdp_10_thou", mod = fit.gdp.pr,
given.values = c("pr_sysYes" = 0)), ylim = c(10,40))
library(gridExtra)
grid.arrange(plot.gdp.pr1, plot.gdp.pr0, ncol = 2)
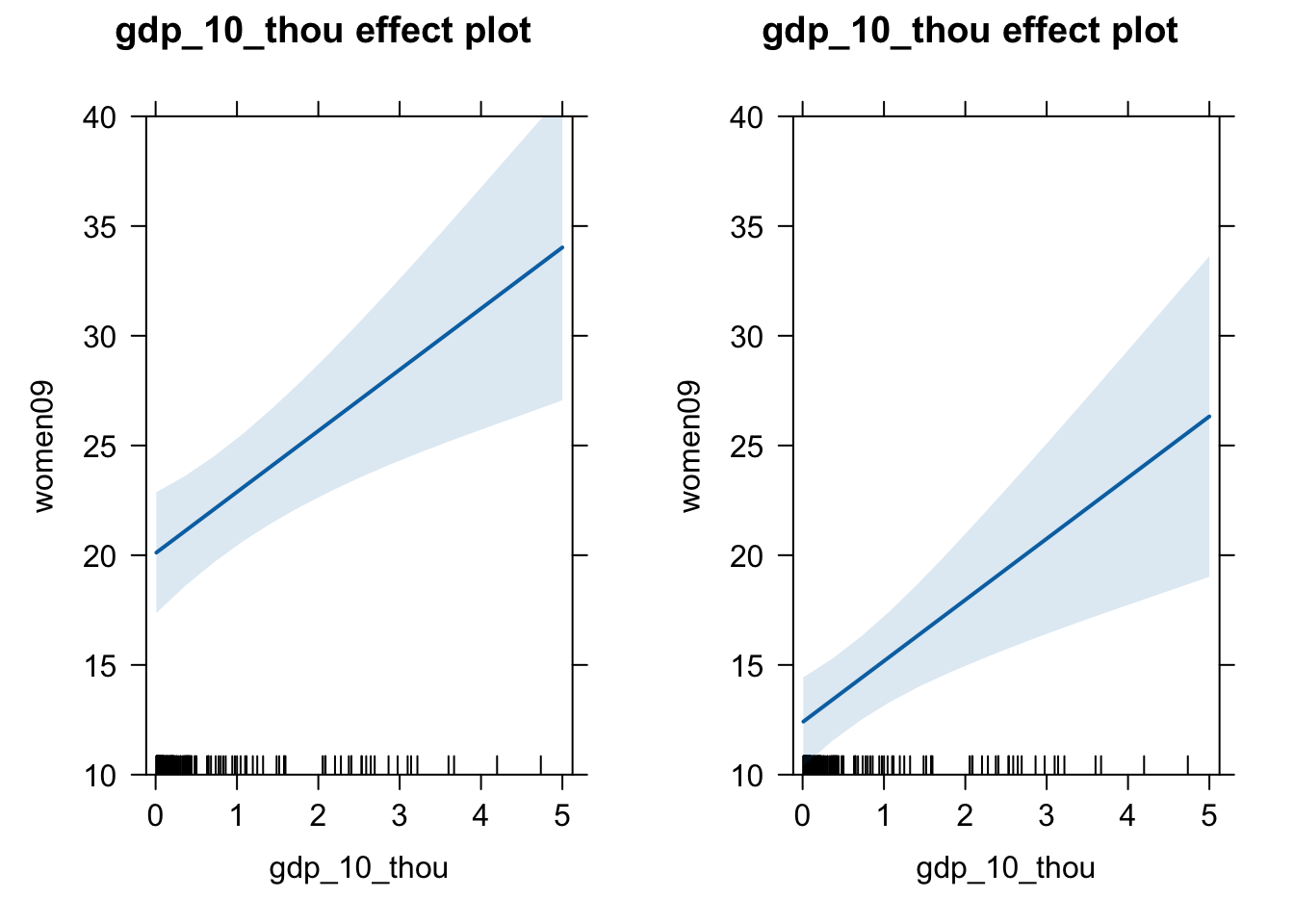
9. Try creating the same graph by providing “gdp_10_thou:pr_sys” as the term.
# plot(effect(term = "gdp_10_thou:pr_sys", mod = fit.gdp.pr))
10. Estimate a regression model of female representation that uses region as the main independent variable.
wd $ Africa <- ifelse(wd $ region == "Africa", 1, 0)
wd $ AsiaPacific <- ifelse(wd $ region == "Asia-Pacific", 1, 0)
wd $ CEEurope <- ifelse(wd $ region == "C&E Europe", 1, 0)
wd $ MiddleEast <- ifelse(wd $ region == "Middle East", 1, 0)
wd $ NAmerica <- ifelse(wd $ region == "N. America", 1, 0)
wd $ SAmerica <- ifelse(wd $ region == "S. America", 1, 0)
wd $ Scandinavia <- ifelse(wd $ region == "Scandinavia", 1, 0)
wd $ WEurope <- ifelse(wd $ region == "W. Europe", 1, 0)
fit.reg <- lm(women09 ~
Africa +
AsiaPacific +
CEEurope +
MiddleEast +
NAmerica +
SAmerica +
Scandinavia +
WEurope + 0,
data = wd )
stargazer(fit.reg, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## Africa 17.560***
## (1.444)
##
## AsiaPacific 12.503***
## (1.713)
##
## CEEurope 16.792***
## (1.938)
##
## MiddleEast 9.489***
## (2.223)
##
## NAmerica 22.367***
## (5.594)
##
## SAmerica 17.984***
## (1.713)
##
## Scandinavia 41.520***
## (4.333)
##
## WEurope 23.753***
## (2.223)
##
## -----------------------------------------------
## Observations 180
## R2 0.785
## Adjusted R2 0.775
## Residual Std. Error 9.690 (df = 172)
## F Statistic 78.317*** (df = 8; 172)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
11. Create an effect plot that shows the relationship between region and female representation.
fit.reg.fac <- lm(women09 ~ region, data = wd)
plot(effect(term = "region", mod = fit.reg.fac))
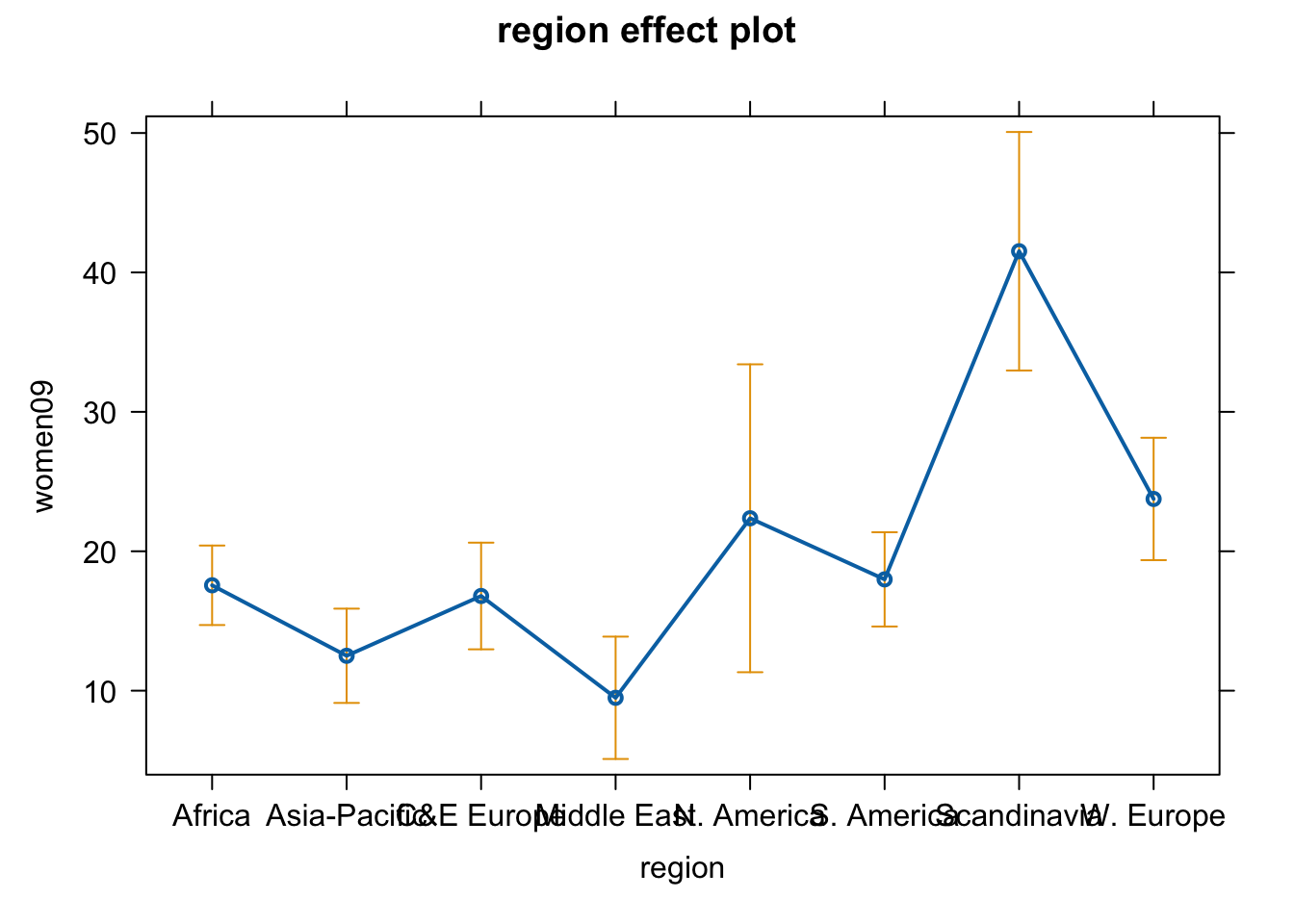
12. Estimate a regression model of female representation on per cpaita GDP that controls for region. Based on the results, can we say per capita GDP is an important determinant of female representation? Why or why not?
fit.reg.gdp <- lm(women09 ~ gdp_10_thou +
Africa +
AsiaPacific +
CEEurope +
MiddleEast +
NAmerica +
SAmerica +
Scandinavia +
WEurope + 0,
data = wd )
stargazer(fit.gdp, fit.reg, fit.reg.gdp, type = "text")
##
## ===========================================================================================
## Dependent variable:
## -----------------------------------------------------------------------
## women09
## (1) (2) (3)
## -------------------------------------------------------------------------------------------
## gdp_10_thou 3.457*** 1.091
## (0.835) (1.271)
##
## Africa 17.560*** 17.714***
## (1.444) (1.419)
##
## AsiaPacific 12.503*** 12.777***
## (1.713) (1.830)
##
## CEEurope 16.792*** 16.483***
## (1.938) (1.910)
##
## MiddleEast 9.489*** 6.647***
## (2.223) (2.472)
##
## NAmerica 22.367*** 19.998***
## (5.594) (6.077)
##
## SAmerica 17.984*** 16.760***
## (1.713) (1.751)
##
## Scandinavia 41.520*** 38.112***
## (4.333) (5.774)
##
## WEurope 23.753*** 20.905***
## (2.223) (3.818)
##
## Constant 14.843***
## (0.954)
##
## -------------------------------------------------------------------------------------------
## Observations 169 180 169
## R2 0.093 0.785 0.795
## Adjusted R2 0.088 0.775 0.784
## Residual Std. Error 10.379 (df = 167) 9.690 (df = 172) 9.380 (df = 160)
## F Statistic 17.139*** (df = 1; 167) 78.317*** (df = 8; 172) 69.005*** (df = 9; 160)
## ===========================================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
13. Estimate a regression model of female representation on frac_eth3, a three-category ordinal variable that measures levels of ethnic fractionalization. In doing so, adopt the dummy variable approach (i.e., treat this variable as a nominal variable).
# Take care of missing values
wd $ frac_eth3[wd $ frac_eth3 == ""] <- NA
# Fix the order
wd $ frac_eth3_ord <- factor(wd $ frac_eth3, levels = c("Low", "Medium", "High"))
# Estimate a model that treats frac_eth3 as a nominal variable:
fit.fr3 <- lm(women09 ~
frac_eth3_ord + 0,
data = wd)
stargazer(fit.fr3, type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## women09
## -----------------------------------------------
## frac_eth3_ordLow 17.457***
## (1.418)
##
## frac_eth3_ordMedium 16.884***
## (1.467)
##
## frac_eth3_ordHigh 17.436***
## (1.442)
##
## -----------------------------------------------
## Observations 177
## R2 0.712
## Adjusted R2 0.707
## Residual Std. Error 11.077 (df = 174)
## F Statistic 143.382*** (df = 3; 174)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
14. Based on the results, do you think ethnic fractionalization levels have a positive/negative impact on female representation?
You may answer this either by looking at the regression table you created above or by creating an effect plot.
# Looking at the regression table, we can see that the predicted values
# of Y for Low, Medium, and High are almost identical -- all of them are
# about 17. This indicates that the ethnic fractionalization levels may
# have little to no impact on female representation.
# Notice that all the three coefficients are highly statistically significant
# (they all have three starts). This only means that the predicted values of
# Y are statistically distinguishable from zero for High, Medium, and Low cases.
# However, what we are looking for here is whether or not predicted value of Y
# for High is different from predicted value of Y for Medium or predicted value
# of Y for Low.
# The numbers we see in the regression table seem to indicate that they are not
# different from each other.
# Let's confirm this by drawing an effect plot.
# Estimate the same model using the original factor variable (for graphs)
fit.fr3.orig <- lm(women09 ~ frac_eth3_ord, data = wd)
plot(effect(term = "frac_eth3_ord", mod = fit.fr3.orig))
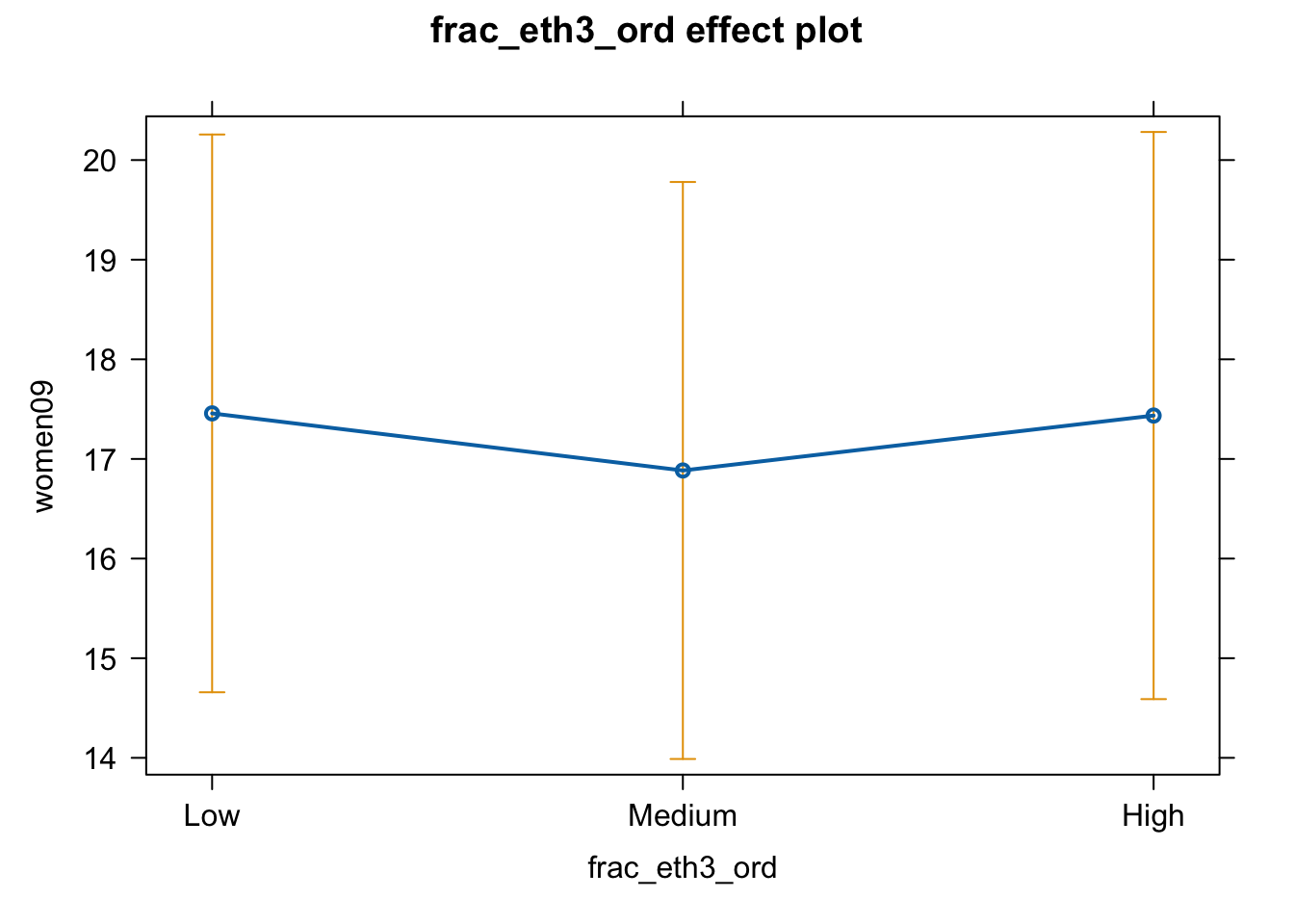
# From the graph, we can clearly see that ethnic fractionalization has
# almost no impact on female representation.